题目内容
如图,△ABC中,∠ACB=90°,CD⊥AB于点D,若BD:AD=1:4,则tan∠BCD的值是 ( )

A. B.
B. C.
C. D.2
D.2
C.
【解析】
试题分析:∵BD:AD=1:4,设BD=x,则
∴AD=4x.
在△ACD和△CBD中,∠A+∠B=90°,∠B+∠BCD=90°,
∴∠CAD=∠BCD.
又∵∠ADC=∠CDB=90°,
∴△ADC∽△CDB.
∴ ,
,
∴CD2=AD•BD.
∴CD=2x.
那么tan∠BCD= .
.
故选C.
考点:1.相似三角形的判定与性质;2.锐角三角函数的定义.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目




 ,则锐角∠A为 ( )
,则锐角∠A为 ( )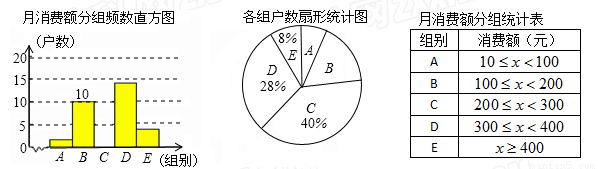

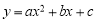 的图象如图所示,则下列结论中错误的是( )
的图象如图所示,则下列结论中错误的是( )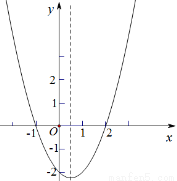
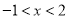 时,
时,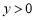
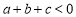
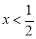 ,y随x的增大而减小
,y随x的增大而减小