题目内容
已知:如图,直角梯形ABCD中,BC//AO,∠A=90°,BC=CD=l0cm,sinC=![]()
(1)求梯形ABCD的面积;
(2)点E、F分别是BC、CD上的动点,点E从点B出发向点C运动,点F从点C出发向点D运动,若两点均以每秒1cm的速度同时出发,连接EF.求△EFC面积的最大值,并说明此时E,F的位置.

解:(1)过点D作DM⊥BC.垂足为M
在Rt△DMC中,DM=CD?sinC=10×![]() =8,
=8,
∴CM=![]()
∴BM=BC―CM=10―6=4.∴AD=4
∴S梯形ABCD=![]() (AD+BC)DM=
(AD+BC)DM=![]() (4+10)×8=56.
(4+10)×8=56.
(2)设运动时间为并秒,则有BE=CF=![]() ,EC=10一
,EC=10一![]() ,
,
过点F作FN⊥BC,垂足为N.
在Rt△FNC中,FN=CF?sinC=![]() ,
,
∴S△EFC=![]() EC?FN=
EC?FN=![]() (10一
(10一![]() )
)![]() =-
=-![]() +4
+4![]() .
.
∴当![]() =
= 时,S△EFC=-
时,S△EFC=-![]() +4 × 5=10.
+4 × 5=10.
即△EFC面积的最大值为10.
此时,点E,F分别在BC,DC的中点处.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
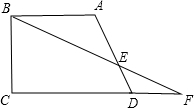 已知:如图,直角梯形ABCD中,∠BCD=90°,∠CDA=60°,AB=AD,AB=4,DF=2,求BF的长.
已知:如图,直角梯形ABCD中,∠BCD=90°,∠CDA=60°,AB=AD,AB=4,DF=2,求BF的长.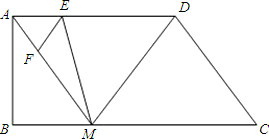 、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.
、F分别是线段AD、AM上的动点(点E与A、D不重合)且∠FEM=∠AMB,设DE=x,MF=y.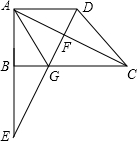
 已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.
已知:如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,以AB为直径的⊙O切DC边于E点,AD=3cm,BC=5cm.求⊙O的面积.