题目内容
完成下列各题：
（1）计算：6tan230°-
sin60°+2tan45°
（2）解方程：x2-2x=5
解：（1）原式=6×
-×
+2×1=2-
+2=
；
（2）由原方程，得
x2-2x+1=5+1，
所以，（x-1）2=6，
开方，得
x-1=±
，
解得，x1=1+，x2=1-．
分析：（1）把特殊角的三角函数值代入，然后计算加减法；
（2）将一元二次方程配成（x+m）2=n的形式，再利用直接开平方法求解．
点评：本题考查了解一元二次方程--配方法，特殊角的三角函数值．
用配方法解一元二次方程的步骤：
（1）形如x2+px+q=0型：第一步移项，把常数项移到右边；第二步配方，左右两边加上一次项系数一半的平方；第三步左边写成完全平方式；第四步，直接开方即可．
（2）形如ax2+bx+c=0型，方程两边同时除以二次项系数，即化成x2+px+q=0，然后配方．
-×+2×1=2-+2=；（2）由原方程，得
x2-2x+1=5+1，
所以，（x-1）2=6，
开方，得
x-1=±
，解得，x1=1+
，x2=1-．分析：（1）把特殊角的三角函数值代入，然后计算加减法；
（2）将一元二次方程配成（x+m）2=n的形式，再利用直接开平方法求解．
点评：本题考查了解一元二次方程--配方法，特殊角的三角函数值．
用配方法解一元二次方程的步骤：
（1）形如x2+px+q=0型：第一步移项，把常数项移到右边；第二步配方，左右两边加上一次项系数一半的平方；第三步左边写成完全平方式；第四步，直接开方即可．
（2）形如ax2+bx+c=0型，方程两边同时除以二次项系数，即化成x2+px+q=0，然后配方．
练习册系列答案
阳光考场单元测试卷系列答案
名校联盟冲刺卷系列答案
名校提分一卷通系列答案
相关题目
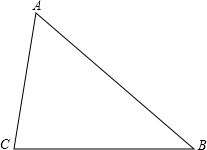如图，在△ABC中，∠B=40°，∠C=80°，按要求完成下列各题：
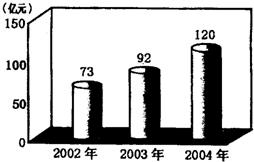下图显示的是今年2月25日《太原日报》刊登的太原市2002年至2004年财政总收入完成情况，图中数据精确到1亿元，根据图中数据完成下列各题：
（2012•泰宁县质检）如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，请按要求完成下列各题：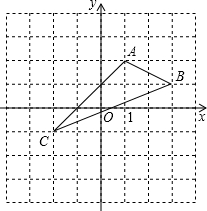
如图，在平面直角坐标系中完成下列各题：