Question

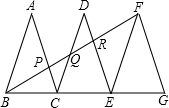
如图，已知△ABC、△DCE、△FEG是三个全等的等腰三角形，底边BC、CE、EG在同一直线上，且AB=

3

，BC=1，连接BF，分别交AC、DC、DE于点P、Q、R．
（1）求证：△BFG∽△FEG，并求出BF的长；
（2）观察图形，请你提出一个与点P相关的问题，并进行解答．（根据提出问题的层次和解答过程评分）

Answer 1

分析：（1）在△BFG中，BG=3BC=3，FG=AB=

3

，在△FEG中，FG=AB=

3

，EG=1，所以有

BG

FG

=

FG

EG

=

3

，且二者有一个公共角∠G，所以可得出两三角形相似．
（2）如果问题较为浅显，可以提问求证：∠PCB=∠REC，这个问题只需要运用两直线平行，同位角相等进行解答．此题为发散性题型，不唯一．

解答：（1）证明：∵△ABC≌△DCE≌△FEG
∴BC=CE=EG=

1

3

BG=1，即BG=3
∴FG=AB=

3

∴

FG

EG

=

BG

FG

=

3

3

=

3

又∠BGF=∠FGE，
∴△BFG∽△FEG，
∵△FEG是等腰三角形，
∴△BFG是等腰三角形，
∴BF=BG=3；

（2）解：A层问题（较浅显的，仅用到了1个知识点）．
例如：①求证：∠PCB=∠REB．（或问∠PCB与∠REB是否相等）等；
②求证：PC∥RE，（或问线段PC与RE是否平行）等．
B层问题（有一定思考的，用到了2～3个知识点）．
例如：①求证：∠BPC=∠BFG等，求证：BP=PR等；
②求证：△ABP∽△CQP等，求证：△BPC∽△BRE等；
③求证：△ABP∽△DQR等；④求BP：PF的值等．
C层问题（有深刻思考的，用到了4个或4以上知识点，或用到了（1）中结论）．
例如：①求证：△ABP≌△ERF；②求证：PQ=RQ等；③求证：△BPC是等腰三角形；
④求证：△PCQ≌△RDQ等；⑤求AP：PC的值等；⑥求BP的长；
⑦求证：PC=

3

3

（或求PC的长）等．
A层解答举例：求证：PC∥RE
证明：△ABC≌△DCE
∴∠PCB=∠REB
∴PC∥RE
B层解答举例：求证：BP=PR
证明：∠ACB=∠REB，
∴AC∥DE．
又BC=CE，∴BP=PR．
C层解答举例：求AP：PC的值．
解：AC∥FG，
∴

PC

FG

=

BC

BG

=

1

3

∴PC=

3

3

，而AC=

3

，
∴AP=

3

-

3

3

=

2 3

3

，
∴AP：PC=2．

点评：此题主要考查了相似三角形的判定，难易程度适中．