题目内容
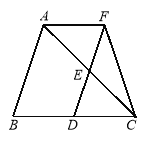
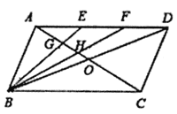
【题目】如图,在![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 是
是![]() 上的点,且
上的点,且![]() . 连接
. 连接![]() 、
、![]() ,使它们分别与
,使它们分别与![]() 相交于点
相交于点![]() .
.
(1)求![]() 的值;
的值;
(2)求证:![]() ;
;
(3)设![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
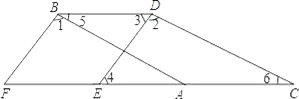
(1)根据平行四边形的性质可得AO=![]() AC,AD=BC,AD∥BC,从而可得△AEG∽△CBG,由AE=EF=FD可得BC=3AE,然后根据相似三角形的性质,即可求出EG:BG的值;
AC,AD=BC,AD∥BC,从而可得△AEG∽△CBG,由AE=EF=FD可得BC=3AE,然后根据相似三角形的性质,即可求出EG:BG的值;
(2)根据相似三角形的性质可得GC=3AG,则有AC=4AG,从而可得AO=![]() AC=2AG,即可得到GO=AO-AG=AG;
AC=2AG,即可得到GO=AO-AG=AG;
(3)根据相似三角形的性质可得AG=![]() AC,AH=
AC,AH=![]() AC,结合AO=
AC,结合AO=![]() AC,即可得到a=
AC,即可得到a=![]() AC,b=
AC,b=![]() AC,c=
AC,c=![]() AC,就可得到a:b:c的值.
AC,就可得到a:b:c的值.
解:(1)因为四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,AO=
,AO=![]() AC,AD=BC,
AC,AD=BC,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)∵![]() ,
,
∴![]() ,
,
易得![]() ,
,
∵![]() ,∴
,∴![]() .
.
(3)∵![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
即![]() .
.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
【题目】“冬桃”是我区某镇的一大特产,现有20箱冬桃,以每箱25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位:千克) |
|
|
| 0 | 0.1 | 0.25 |
箱数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)20箱冬桃中,与标准质量差值为﹣0.2千克的有 筐,最重的一箱重 千克
(2)与标准重量比较,20箱冬桃总计超过多少千克?
(3)若冬桃每千克售价3元,则出售这20箱冬桃可卖多少元?