Question

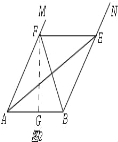
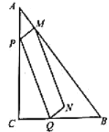
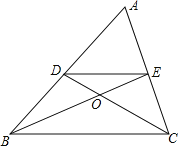
【题目】如图，在梯形ABCD中，点E，F分别在边AB，CD上，AD∥EF∥BC，EF与BD交于点G，AD＝5，BC＝10，＝．

（1）求EF的长；

（2）设＝，＝，那么＝　 　，＝　 　．（用向量、表示）

Answer 1

【答案】（1）7；（2）﹣，+．

【解析】

（1）由平行线得出，△BEG∽△BAD，△DFG∽△DCB，得出，，可解得EG＝3，GF＝4，即可得出答案；

（2）求出＝＝，得出＝+＝﹣，得出＝＝﹣+＝+，证出FC＝DC，得出＝得出结果．

解：（1）∵＝，∴＝,=.

∵AD∥EF∥BC，

∴，△BEG∽△BAD，△DFG∽△DCB，

∴，，

即，，

解得：EG＝3，GF＝4，

∴EF＝EG+GF＝7；

（2）∵AD＝5，BC＝10，

∴AD＝BC，

∵AD∥EF∥BC，

∴＝＝，

∴＝+＝﹣，

∴＝＝﹣+＝+，

∵，

∴=，

∴FC＝DC，

∴＝＝（+）＝+；

故答案为：﹣，+．