题目内容
如图,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为( )
A.

B.

C.

D.

【答案】分析:算出阴影部分的面积及大正方形的面积,这个比值就是所求的概率.
解答: 解:设小正方形的边长为1,则其面积为1.
解:设小正方形的边长为1,则其面积为1.
∵圆的直径正好是大正方形边长,
∴根据勾股定理,其小正方形对角线为 ,即圆的直径为
,即圆的直径为 ,
,
∴大正方形的边长为 ,
,
则大正方形的面积为 ×
× =2,则小球停在小正方形内部(阴影)区域的概率为
=2,则小球停在小正方形内部(阴影)区域的概率为 .
.
故选C.
点评:用到的知识点为:概率=相应的面积与总面积之比;难点是得到两个正方形的边长的关系.
解答:
 解:设小正方形的边长为1,则其面积为1.
解:设小正方形的边长为1,则其面积为1.∵圆的直径正好是大正方形边长,
∴根据勾股定理,其小正方形对角线为
 ,即圆的直径为
,即圆的直径为 ,
,∴大正方形的边长为
 ,
,则大正方形的面积为
 ×
× =2,则小球停在小正方形内部(阴影)区域的概率为
=2,则小球停在小正方形内部(阴影)区域的概率为 .
.故选C.
点评:用到的知识点为:概率=相应的面积与总面积之比;难点是得到两个正方形的边长的关系.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 如图,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为( )
如图,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
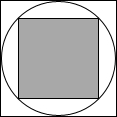 (2013•烟台模拟)如图,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为
(2013•烟台模拟)如图,小明随意向水平放置的大正方形内部区域抛一个小球,则小球停在小正方形内部(阴影)区域的概率为








