题目内容
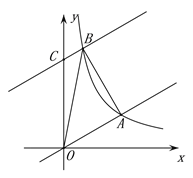
【题目】如图,在平面直角坐标系xOy中,直线y=![]() x与反比例函数y=k/x在第一象限内的图象相交于点A(m,3).
x与反比例函数y=k/x在第一象限内的图象相交于点A(m,3).
(1)求该反比例函数的关系式;
(2)将直线y=![]() x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B,连接AB,这时恰好AB⊥OA,求tan∠AOB的值;
(3)在(2)的条件下,在射线OA上存在一点P,使△PAB∽△BAO,求点P的坐标.
【答案】(1) y=![]() (2)
(2) ![]() (3) P(7
(3) P(7![]() ,7)
,7)
【解析】(1)、首先根据一次函数的解析式求出点A的坐标,然后将点A代入反比例函数解析式得出k的值;(2)、首先得出平移后的解析式,然求出直线AB的解析式,得出AB和OA的长度,从而得出答案;(3)、根据△APB和△ABO相似得出AP和OP的长度,从而得出点P的坐标.
(1)、∵点A(m,3)在直线y=![]() x上, ∴3=
x上, ∴3=![]() m,m=
m,m=![]() ,∴点A(
,∴点A(![]() ,3)
,3)
∵点A(![]() ,3)在反比例函数y=
,3)在反比例函数y=![]() 上,∴k=
上,∴k=![]() ×3=
×3=![]() , ∴y=
, ∴y=![]() ;
;
(2)、直线向上平移8个单位后表达式为:y=![]() x +8
x +8
∵AB⊥OA,直线AB过点A(![]() ,3), ∴直线AB解析式:
,3), ∴直线AB解析式:![]() ,
,
∴![]() . ∴x=
. ∴x=![]() .∴B(
.∴B(![]() ,9) ,∴AB=4
,9) ,∴AB=4![]() ;
;
又∵OA=6,∴tan∠AOB=![]() ;
;
(3)、∵△APB∽△ABO ,∴![]() , 即
, 即![]() ,
,
∴AP=8, ∴OP=14, ∴P(7![]() ,7).
,7).

练习册系列答案
相关题目