Question

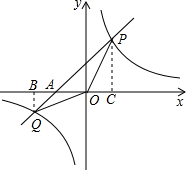如图，已知反比例函数y=

12

x

的图象与一次函数y=kx+4的图象相交于点P、Q，且一次函数y=kx+4的图象与x轴交于点A；若P的纵坐标为6，PC垂直x轴，QB垂直y轴．
求：（1）一次函数的解析式．
（2）△POQ的面积．

Answer 1

分析：（1）由于反比例函数y=

12

x

的图象与一次函数y=kx+4的图象相交于点P、而P的纵坐标为6，由此可以求出P的横坐标，然后代入一次函数的解析式即可求解；
（2）利用一次函数和反比例函数解析式组成方程组求解得到Q的坐标，然后利用面积的割补法即可解决问题．

解答：解：（1）∵反比例函数y=

12

x

的图象与一次函数y=kx+4的图象相交于点P、Q，
而P的纵坐标为6，
∴P的横坐标为2，
∴P的坐标为（2，6），
∴6=2k+4，
∴k=1，
∴y=x+4；

（2）解方程组

y=x+4 y= 12 x

得

x=2 y=6

或

x=-6 y=-2

，
∴Q的坐标为（-6，-2），
当y=0时，x+4=0，
∴x=-4，
∴A的坐标为（-4，0），
∴S_△POQ=S_△AOQ+S_△POA=16．

点评：本题综合考查反比例函数与方程组的相关知识点．先由点的坐标求函数解析式，然后解由解析式组成的方程组求出交点的坐标，体现了数形结合的思想．