��Ŀ����
��֪����x�Ķ��κ���y=x2﹣2mx+m2+m��ͼ�������x�ĺ���y=kx+1��ͼ��������A��x1��y1����B��x2��y2������x1��x2��
��1����k=1��m=0��1ʱ����AB�ij���
��2����k=1��mΪ�κ�ֵʱ������AB�ij��Ƿ䣿��֤����IJ��룮
��3����m=0������kΪ��ֵʱ�������AOB����״��֤����IJ��룮
��ƽ���������ľ��빫ʽ![]() ����
����
���㣺
���κ����ۺ��⣮
������
��1���Ƚ�k=1��m=0�ֱ���룬�ó����κ����Ľ���ʽΪy=x2��ֱ�ߵĽ���ʽΪy=x+1������![]() ����x2﹣x﹣1=0������һԪ���η��̸���ϵ���Ĺ�ϵ�õ�x1+x2=1��x1•x2=﹣1������A��B�ֱ���x�ᡢy���ƽ���ߣ����߽��ڵ�C��֤����ABC�ǵ���ֱ�������Σ����ݹ��ɶ����ó�AB=
����x2﹣x﹣1=0������һԪ���η��̸���ϵ���Ĺ�ϵ�õ�x1+x2=1��x1•x2=﹣1������A��B�ֱ���x�ᡢy���ƽ���ߣ����߽��ڵ�C��֤����ABC�ǵ���ֱ�������Σ����ݹ��ɶ����ó�AB=![]() AC�������������빫ʽ����ȫƽ����ʽ���AB=
AC�������������빫ʽ����ȫƽ����ʽ���AB=![]() ��ͬ������k=1��m=1ʱ��AB=
��ͬ������k=1��m=1ʱ��AB=![]() ��
��
��2����k=1��mΪ�κ�ֵʱ������![]() ����x2﹣��2m+1��x+m2+m﹣1=0������һԪ���η��̸���ϵ���Ĺ�ϵ�õ�x1+x2=2m+1��x1•x2=m2+m﹣1��ͬ��1�������AB=
����x2﹣��2m+1��x+m2+m﹣1=0������һԪ���η��̸���ϵ���Ĺ�ϵ�õ�x1+x2=2m+1��x1•x2=m2+m﹣1��ͬ��1�������AB=![]() ��
��
��3����m=0��kΪ���ⳣ��ʱ��������������ۣ��ٵ�k=0ʱ����![]() ����A��﹣1��1����B��1��1������Ȼ��AOBΪֱ�������Σ��ڵ�k=1ʱ������
����A��﹣1��1����B��1��1������Ȼ��AOBΪֱ�������Σ��ڵ�k=1ʱ������![]() ����x2﹣x﹣1=0������һԪ���η��̸���ϵ���Ĺ�ϵ�õ�x1+x2=1��x1•x2=﹣1��ͬ��1�����AB=
����x2﹣x﹣1=0������һԪ���η��̸���ϵ���Ĺ�ϵ�õ�x1+x2=1��x1•x2=﹣1��ͬ��1�����AB=![]() ����AB2=10�����������ľ��빫ʽ����ȫƽ����ʽ���OA2+OB2=10���ɹ��ɶ������涨���ж���AOBΪֱ�������Σ��۵�kΪ����ʵ��ʱ������
����AB2=10�����������ľ��빫ʽ����ȫƽ����ʽ���OA2+OB2=10���ɹ��ɶ������涨���ж���AOBΪֱ�������Σ��۵�kΪ����ʵ��ʱ������![]() ����x2﹣kx﹣1=0������һԪ���η��̸���ϵ���Ĺ�ϵ�õ�x1+x2=k��x1•x2=﹣1�������������빫ʽ����ȫƽ����ʽ���AB2=k4+5k2+4��OA2+OB2═k4+5k2+4���ɹ��ɶ������涨���ж���AOBΪֱ�������Σ�
����x2﹣kx﹣1=0������һԪ���η��̸���ϵ���Ĺ�ϵ�õ�x1+x2=k��x1•x2=﹣1�������������빫ʽ����ȫƽ����ʽ���AB2=k4+5k2+4��OA2+OB2═k4+5k2+4���ɹ��ɶ������涨���ж���AOBΪֱ�������Σ�
���
�⣺��1����k=1��m=0ʱ����ͼ��
��![]() ��x2﹣x﹣1=0��
��x2﹣x﹣1=0��
��x1+x2=1��x1•x2=﹣1��
����A��B�ֱ���x�ᡢy���ƽ���ߣ����߽��ڵ�C��
��ֱ��AB�Ľ���ʽΪy=x+1��
���BAC=45�㣬��ABC�ǵ���ֱ�������Σ�
��AB=![]() AC=
AC=![]() |x2﹣x1|=
|x2﹣x1|=![]()
![]() =
=![]() ��
��
ͬ������k=1��m=1ʱ��AB=![]() ��
��
��2�����룺��k=1��mΪ�κ�ֵʱ��AB�ij����䣬��AB=![]() ���������£�
���������£�
��![]() ����x2﹣��2m+1��x+m2+m﹣1=0��
����x2﹣��2m+1��x+m2+m﹣1=0��
��x1+x2=2m+1��x1•x2=m2+m﹣1��
��AB=![]() AC=
AC=![]() |x2﹣x1|=
|x2﹣x1|=![]()
![]() =
=![]() ��
��
��3����m=0��kΪ���ⳣ��ʱ����AOBΪֱ�������Σ��������£�
�ٵ�k=0ʱ��������ͼ��Ϊֱ��y=1��
��![]() ����A��﹣1��1����B��1��1����
����A��﹣1��1����B��1��1����
��Ȼ��AOBΪֱ�������Σ�
�ڵ�k=1ʱ����һ�κ���Ϊֱ��y=x+1��
��![]() ����x2﹣x﹣1=0��
����x2﹣x﹣1=0��
��x1+x2=1��x1•x2=﹣1��
��AB=![]() AC=
AC=![]() |x2﹣x1|=
|x2﹣x1|=![]()
![]() =
=![]() ��
��
��AB2=10��
��OA2+OB2=x12+y12+x22+y22
=x12+x22+y12+y22
=x12+x22+��x1+1��2+��x2+1��2
=x12+x22+��x12+2x1+1��+��x22+2x2+1��
=2��x12+x22��+2��x1+x2��+2
=2��1+2��+2��1+2
=10��
��AB2=OA2+OB2��
���AOB��ֱ�������Σ�
�۵�kΪ����ʵ������AOB��Ϊֱ�������Σ�
��![]() ����x2﹣kx﹣1=0��
����x2﹣kx﹣1=0��
��x1+x2=k��x1•x2=﹣1��
��AB2=��x1﹣x2��2+��y1﹣y2��2
=��x1﹣x2��2+��kx1﹣kx2��2
=��1+k2����x1﹣x2��2
=��1+k2��[��x1+x2��2﹣4x1•x2]
=��1+k2����4+k2��
=k4+5k2+4��
��OA2+OB2=x12+y12+x22+y22
=x12+x22+y12+y22
=x12+x22+��kx1+1��2+��kx2+1��2
=x12+x22+��k2x12+2kx1+1��+��k2x22+2kx2+1��
=��1+k2����x12+x22��+2k��x1+x2��+2
=��1+k2����k2+2��+2k•k+2
=k4+5k2+4��
��AB2=OA2+OB2��
���AOBΪֱ�������Σ�
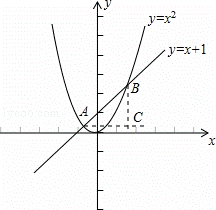
������
���⿼���˶��κ������ۺ����ͣ������漰����֪ʶ����һԪ���η��̸���ϵ���Ĺ�ϵ��ƽ���������ľ��빫ʽ����ȫƽ����ʽ�����ɶ������涨������һ���Ѷȣ������ʽ�ӵı�������Ҫ��ϸߣ������������һ���˼�룮

 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�