题目内容
已知函数y=-9x2-6ax+2a-a2,当-| 1 |
| 3 |
| 1 |
| 3 |
分析:本题是关于二次函数最值的“逆向问题”,由题设知,二次函数y=-9x2-6ax-a2+2a的对称轴是x=-
,而x的取值范围是-
≤x≤
,所以要对-
是否在x的取值范围内讨论求解.
| a |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| a |
| 3 |
解答:解:(1)若-
≤-
≤
,即-1≤a≤1,抛物线开口向下,当x=-
时,y最大值=2a,
∵二次函数最大值-3,即a=-
与-1≤a≤1矛盾,舍去.
(2)若-
<-
,即a>1
当-
≤x≤
时,y随x增大而减小,当x=-
时,y最大值=-a2+4a-1,
由-a2+4a-1=-3,解得a=2±
又a>1,∴a=2+
(3)若-
>
,即a<-1
当-
≤x≤
时,y随x增大而增大,当x=
时,y最大值=-a2-1,
由-a2-1=-3,解得a=±
又a<-1,∴a=-
综上所述,a=2+
或a=-
.
| 1 |
| 3 |
| a |
| 3 |
| 1 |
| 3 |
| a |
| 3 |
∵二次函数最大值-3,即a=-
| 3 |
| 2 |
(2)若-
| a |
| 3 |
| 1 |
| 3 |
当-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
由-a2+4a-1=-3,解得a=2±
| 6 |
又a>1,∴a=2+
| 6 |
(3)若-
| a |
| 3 |
| 1 |
| 3 |
当-
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
由-a2-1=-3,解得a=±
| 2 |
又a<-1,∴a=-
| 2 |
综上所述,a=2+
| 6 |
| 2 |
点评:本题考查了二次函数的最值,难度适中,关键是掌握用分类讨论的思想进行解题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
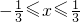 时,y的最大值为-3,求a.
时,y的最大值为-3,求a. 时,y的最大值为-3,求a.
时,y的最大值为-3,求a.