题目内容
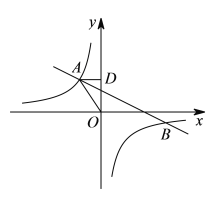
【题目】如图,在平面直角坐标系中,反比例函数![]()
![]() 与一次函数
与一次函数![]() 交于第二、四象限的
交于第二、四象限的![]() ,
,![]() 两点,过点
两点,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求反比例函数和一次函数的解析式;
(2)请根据图象直接写出![]() 的自变量
的自变量![]() 的取值范围.
的取值范围.
【答案】(1) 反比例函数的解析式为y=﹣![]() ,一次函数的解析式为y=﹣
,一次函数的解析式为y=﹣![]() x+2.(2)x≤﹣2或0<x≤6.
x+2.(2)x≤﹣2或0<x≤6.
【解析】
(1)根据S△AOD=3可得AD=2,根据反比例函数的特点k=xy为定值,列出方程,求出k的值,便可求出反比例函数的解析式;根据k的值求出B点的坐标,用待定系数法便可求出一次函数的解析式.
(2)根据函数图象可直接解答.
(1)∵AD⊥y轴于点D,OD=3,
∴![]() ,
,
∴AD=2.即A(﹣2,3),
将A点坐标代入y=![]() (k≠0),得k=﹣2×3=﹣6.
(k≠0),得k=﹣2×3=﹣6.
反比例函数的解析式为y=﹣![]() .
.
将B点坐标代入y=﹣![]() 中,得﹣1=﹣
中,得﹣1=﹣![]() ,解得n=6.即B(6,﹣1),
,解得n=6.即B(6,﹣1),
将A、B两点坐标代入y=ax+b,得![]() ,解得
,解得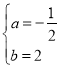 .
.
所以一次函数的解析式为y=﹣![]() x+2.
x+2.
(2)ax+b≥![]() 的自变量x的取值范围是x≤﹣2或0<x≤6.
的自变量x的取值范围是x≤﹣2或0<x≤6.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
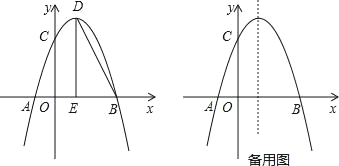
【题目】抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
从上表可知,下列说法正确的有多少个
①抛物线与x轴的一个交点为(﹣2,0);
②抛物线与y轴的交点为(0,6);
③抛物线的对称轴是直线x=![]() ;
;
④抛物线与x轴的另一个交点为(3,0);
⑤在对称轴左侧,y随x增大而减少.
A. 2 B. 3 C. 4 D. 5