题目内容
 如图所示,梯形ABCD中,AB∥CD,两对角线AC、BD交于0点,且BD⊥AD,已知BC=CD=7,则AB=
如图所示,梯形ABCD中,AB∥CD,两对角线AC、BD交于0点,且BD⊥AD,已知BC=CD=7,则AB=14
14
.分析:首先过C作CE∥AD,可得四边形ADCE是平行四边形,进而得到AE=7,再证明CM⊥DB,根据等腰三角形的性质证明△ECB是等腰三角形,进而得到EB=CB=7.
解答: 解:过C作CE∥AD,
解:过C作CE∥AD,
∵DC∥AB,
∴四边形ADCE是平行四边形,
∴AE=DC=7,
∵BD⊥AD,
∴∠ADB=90°,
∵AD∥BC,
∴∠EMB=∠ADB=90°,
∴CM⊥DB,
∵DC=BC,
∴△DCB是等腰三角形,
∴∠1=∠2,
∵DC∥AB,
∴∠1=∠3,
∴∠2=∠3,
∴EB=CB=7,
∴AB=7+7=14,
故答案为:14.
 解:过C作CE∥AD,
解:过C作CE∥AD,∵DC∥AB,
∴四边形ADCE是平行四边形,
∴AE=DC=7,
∵BD⊥AD,
∴∠ADB=90°,
∵AD∥BC,
∴∠EMB=∠ADB=90°,
∴CM⊥DB,
∵DC=BC,
∴△DCB是等腰三角形,
∴∠1=∠2,
∵DC∥AB,
∴∠1=∠3,
∴∠2=∠3,
∴EB=CB=7,
∴AB=7+7=14,
故答案为:14.
点评:此题主要考查了梯形的性质,以及等腰三角形的判定与性质,关键是掌握等腰三角形三线合一的性质.

练习册系列答案
相关题目
 如图所示,在△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线.
如图所示,在△ABC中,AB=AC,BD,CE分别为∠ABC,∠ACB的平分线. 已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4
已知:如图所示,梯形ABCD中,AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4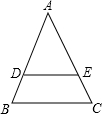 如图所示,在△ABC中,DE∥BC,△ADE和梯形DBCE的面积相等,则AD:DB=
如图所示,在△ABC中,DE∥BC,△ADE和梯形DBCE的面积相等,则AD:DB=
 梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为
梯形的边运动,设点P运动的路程为x,△ABP的面积为y,函数图象如图②所示,则△ABC面积为