题目内容
若 ,且a+b+c≠0,则k的值为
,且a+b+c≠0,则k的值为
- A.

- B.-1
- C.1
- D.-

B
分析:由已知可得:a-2b=kc,b-2c=ka,c-2a=kb;三式相加,即可求得k的值.
解答:由题意,得:
a-2b=kc;…①
b-2c=ka;…②
c-2a=kb;…③
①+②+③得:
k(a+b+c)=a-2b+b-2c+c-2a=a+b+c-(2a+2b+2c)=-(a+b+c);
∵a+b+c≠0,
∴k= =-1.故选B.
=-1.故选B.
点评:解答此类题一定要熟练掌握分式的基本性质.
分析:由已知可得:a-2b=kc,b-2c=ka,c-2a=kb;三式相加,即可求得k的值.
解答:由题意,得:
a-2b=kc;…①
b-2c=ka;…②
c-2a=kb;…③
①+②+③得:
k(a+b+c)=a-2b+b-2c+c-2a=a+b+c-(2a+2b+2c)=-(a+b+c);
∵a+b+c≠0,
∴k=
 =-1.故选B.
=-1.故选B.点评:解答此类题一定要熟练掌握分式的基本性质.

练习册系列答案
相关题目


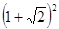 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
 (其中
(其中 均为整数),则有
均为整数),则有
 . ∴
. ∴ ,
, .
. 的式子化为平方式的方法.
的式子化为平方式的方法.
 ,用含
,用含 的式子分别表示
的式子分别表示 ,得
,得 =_ ,
=_ , =_ ;
=_ ; ;
;
 均为正整数,求a的值.
均为正整数,求a的值. AC长为半径作
AC长为半径作 ⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC. ,且AC=4,求CF的长.
,且AC=4,求CF的长.
 是⊙
是⊙ 上一点,⊙
上一点,⊙ 相交于
相交于 、
、 两点,
两点, ,垂足为
,垂足为 、
、 两点,延长
两点,延长 交⊙
交⊙ ,交
,交 的延长线于
的延长线于 ,
, 交
交 于
于 ,连结
,连结 .
. ;
; ,求证:
,求证: ;
; ,且线段
,且线段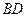 、
、 的长是关于
的长是关于 的方程
的方程 的两个实数根,求
的两个实数根,求
 AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连结AE、AD、DC. ,且AC=4,求CF的长.
,且AC=4,求CF的长.