题目内容
如图，已知△ABC、△DCE、△FEG是三个全等的等腰三角形，底边BC、CE、EG在同一直线上，且AB=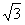
，BC=1。连结BF，分别交AC、DC、DE于点P、Q、R。
（1）求证：△BFG∽△FEG；
（2）求出BF的长。
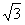，BC=1。连结BF，分别交AC、DC、DE于点P、Q、R。（1）求证：△BFG∽△FEG；
（2）求出BF的长。
解：（1）证明∵△ABC、△DCE、△FEG是三个全等的等腰三角形
∴FG=AB=
， GE=BC=1， BG=3BC=3
∴
=
，
=
=
，∴
=
∵∠FGE=∠BGF ∴△BFG∽△FEG
（2）由（1）知：△BFG∽△FEG
∴
=
∵FG=FE ∴BF=BG=3
∴FG=AB=
， GE=BC=1， BG=3BC=3 ∴
=，==，∴=∵∠FGE=∠BGF ∴△BFG∽△FEG
（2）由（1）知：△BFG∽△FEG
∴
=∵FG=FE ∴BF=BG=3
练习册系列答案
名校课堂系列答案
相关题目
24、如图，已知△ABC和△CDE均为等边三角形，且点B、C、D在同一条直线上，连接AD、BE，交CE和AC分别于G、H点，连接GH．
如图，已知△ABC，∠ACB=90°，AC=BC，点E、F在AB上，∠ECF=45°．
17、（1）已知线段a，h，用直尺和圆规作等腰三角形ABC，底边BC=a，BC边上的高为h（要求尺规作图，不写作法和证明）
20、如图，已知△ABC是锐角三角形，且∠A=50°，高BE、CF相交于点O，求∠BOC的度数．