题目内容
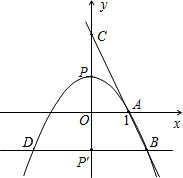
已知抛物线 与它的对称轴相交于点
与它的对称轴相交于点 ,与
,与 轴交于
轴交于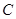 ,与
,与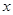 轴正半轴交于
轴正半轴交于 .
.
(1)求这条抛物线的函数关系式;
(2)设直线 交
交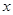 轴于
轴于 是线段
是线段 上一动点(
上一动点( 点异于
点异于 ),过
),过 作
作 轴交直线
轴交直线 于
于 ,过
,过 作
作 轴于
轴于 ,求当四边形
,求当四边形 的面积等于
的面积等于 时点
时点 的坐标.
的坐标.
解:(1)由题意,知点 是抛物线的顶点,
是抛物线的顶点,
 ,
, ,
, 抛物线的函数关系式为
抛物线的函数关系式为 .
.
(2)由(1)知,点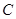 的坐标是
的坐标是 .设直线
.设直线 的函数关系式为
的函数关系式为 ,
,
则
 ,
, ,
, .
.
由 ,得
,得 ,
, ,
, 点
点 的坐标是
的坐标是 .
.
设直线 的函数关系式是
的函数关系式是 ,
,
则 解得
解得 ,
, .
. 直线
直线 的函数关系式是
的函数关系式是 .
.
设 点坐标为
点坐标为 ,则
,则 .
. 轴,
轴, 点的纵坐标也是
点的纵坐标也是 .
.
设 点坐标为
点坐标为 ,
, 点
点 在直线
在直线 上,
上, ,
, .
. 轴,
轴, 点的坐标为
点的坐标为 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,当
,当 时,
时, ,
,
而 ,
, ,
, 点坐标为
点坐标为 和
和 .
.
解析

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 探究线段CA与CB的比值:
探究线段CA与CB的比值:

