题目内容
如图所示,是函数y=kx+b在平面直角坐标系中的图象.
(1)根据图象,求k,b的值;
(2)在图中画出函数y=﹣2x+2的图象;
(3)x为何值时函数y=kx+b的值大于函数y=﹣2x+2的值;
(4)求两直线与x轴围成的三角形的面积.

| 解:(1)∵直线经过(﹣2,0)(0,2), ∴  , ,解得  ; ;(2)如右图: 当x=0时,y=2;当y=0时,﹣2x+2=0, 解得:x=1, ∴y=﹣2x+2经过(0,2)(1,0); (3)根据图象,当x>0时, 函数y=kx+b的值大于函数y=﹣2x+2的值; (4)根据图象, 三角形在x轴上的边长是|﹣2|+1=3,高为2, ∴面积=  ×3×2=3. ×3×2=3. |
 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,是函数y=kx+b在平面直角坐标系中的图象.
如图所示,是函数y=kx+b在平面直角坐标系中的图象.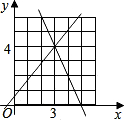 如图所示的是函数y=kx+b,y=mx+n的图象,
如图所示的是函数y=kx+b,y=mx+n的图象,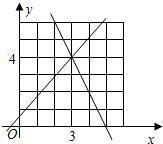 如图所示的是函数y=kx+b与y=mx+n的图象,求方程组
如图所示的是函数y=kx+b与y=mx+n的图象,求方程组 18、如图所示的是函数y=kx+b与y=mx+b的图象,则关于x的不等式kx+b>mx+n的解集是
18、如图所示的是函数y=kx+b与y=mx+b的图象,则关于x的不等式kx+b>mx+n的解集是 如图所示的是函数y1=kx+b与y2=mx+n的图象,
如图所示的是函数y1=kx+b与y2=mx+n的图象,