Question

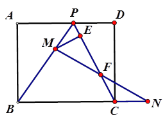
【题目】如图，在矩形ABCD中，AD=10，AB=8，点P在AD上，且BP=BC，点M在线段BP上，点N在线段BC的延长线上，且MP=NC，连接MN交线段PC于点F，过点M作ME⊥PC于点E，则EF= _______.

Answer 1

【答案】

【解析】

过点M作MH∥BC交CP于H，根据两直线平行，同位角相等可得∠MHP=∠BCP，两直线平行，内错角相等可得∠NCF=∠MHF，根据等边对等角可得∠BCP=∠BPC，然后求出∠BPC=∠MHP，根据等角对等边可得PM=MH，根据等腰三角形三线合一的性质可得PE=EH，利用“角边角”证明△NCF和△MHF全等，根据全等三角形对应边相等可得CF=FH，从而求出EF=CP，根据矩形的对边相等可得BC=AD=10，再利用勾股定理列式求出AP，然后求出PD，再次利用勾股定理列式计算即可求出CP，从而得解．

如图,过点M作MH∥BC交CP于H，

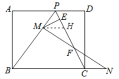
则∠MHP=∠BCP，∠NCF=∠MHF，
∵BP=BC，
∴∠BCP=∠BPC，
∴∠BPC=∠MHP，
∴PM=MH，
∵PM=CN，
∴CN=MH，
∵ME⊥CP,
∴PE=EH，
在△NCF和△MHF中，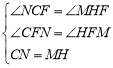
，
∴△NCF≌△MHF(AAS)，
∴CF=FH，
∴EF=EH+FH=CP，
∵矩形ABCD中，AD=10，
∴BC=AD=10，
∴BP=BC=10，
在Rt△ABP中,AP===6，
∴PD=ADAP=106=4，
在Rt△CPD中,CP===，
∴EF=CP=×=.
故答案为：.