题目内容
已知：如图，四边形ABCD中，AB=DC，∠B=∠C．求证：∠A=∠D．
证明：分别延长BA、CD，交点为P，如图，
∵∠B=∠C，
∴PB=PC，
∵AB=DC，
∴PA=PD，
∴∠PAD=∠PDA，
∵∠PAD+∠BAD=180°，∠PDA+∠CDA=180°，
∴∠BAD=∠CDA．
分析：如图，分别延长BA、CD，交点为P，由∠B=∠C利用等腰三角形的性质判定得到PB=PC，而AB=DC，由此得到PA=PD，
接着利用等腰三角形的性质得到∠PAD=∠PDA，然后利用三角形的内角和即可证明题目的结论．
点评：此题主要考查了等腰三角形的性质和判定，解题的关键是通过作辅助线把四边形的问题转化为等腰三角形的问题解决问题．
∵∠B=∠C，
∴PB=PC，
∵AB=DC，
∴PA=PD，
∴∠PAD=∠PDA，
∵∠PAD+∠BAD=180°，∠PDA+∠CDA=180°，
∴∠BAD=∠CDA．
分析：如图，分别延长BA、CD，交点为P，由∠B=∠C利用等腰三角形的性质判定得到PB=PC，而AB=DC，由此得到PA=PD，
接着利用等腰三角形的性质得到∠PAD=∠PDA，然后利用三角形的内角和即可证明题目的结论．
点评：此题主要考查了等腰三角形的性质和判定，解题的关键是通过作辅助线把四边形的问题转化为等腰三角形的问题解决问题．
练习册系列答案
天天练口算系列答案
相关题目
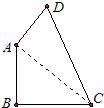已知，如图，四边形ABCD中∠B=90°，AB=9，BC=12，AD=8，CD=17．
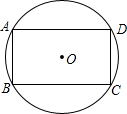已知：如图，四边形ABCD内接于⊙O，且AB∥CD，AD∥BC，
已知，如图，四边形ABCD是正方形，E、F分别是AB和AD延长线上的点，且BE=DF
已知：如图，四边形ABCD中，BC=CD=10，AB=15，AB⊥BC，CD⊥BC，若把四边形ABCD绕直线AB旋转一周，则所得几何体的表面积是多少？
已知：如图，四边形ABCD及一点P．