Question

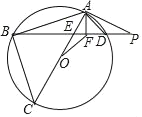
【题目】如图，△ABC内接于半径为的⊙O，AC为直径，AB＝，弦BD与AC交于点E，点P为BD延长线上一点，且∠PAD＝∠ABD，过点A作AF⊥BD于点F，连接OF．

（1）求证：AP是⊙O的切线；

（2）求证：∠AOF＝∠PAD；

（3）若tan∠PAD＝，求OF的长．

Answer 1

【答案】（1）证明见解析（2）见解析（3）

【解析】

（1）根据圆周角定理得到∠ABC＝90°，推出PA⊥AC，于是得到AP是⊙O的切线；

（2）解直角三角形得到∠C＝45°，求得FA＝FD，连接OD，根据全等三角形的性质得到∠AOF＝∠DOF，于是得到结论；

（3）延长OF交AD于点G，根据等腰三角形的性质得到OG⊥AD，解直角三角形即可得到结论．

（1）证明：∵AC是⊙O的直径，

∴∠ABC＝90°，

即∠ABD+∠CBD＝90°，

∵，

∴∠CAD＝∠CBD，

∵∠PAD＝∠ABD，

∴∠PAD+∠CAD＝∠ABD+∠CBD＝90°，

即PA⊥AC，

∵AC是⊙O的直径，

∴AP是⊙O的切线；

（2）解：∵在Rt△ABC中，，

∴sinC＝，

∴∠C＝45°，

∵，

∴∠ADB＝∠C＝45°，

∵AF⊥BD，

∴∠FAD＝∠ADB＝45°，

∴FA＝FD，

连接OD，

∵OA＝OD，OF＝OF，FA＝FD，

∴△AOF≌△DOF（SSS），

∴∠AOF＝∠DOF，

∴∠AOD＝2∠AOF，

∵，

∴∠AOD＝2∠ABD，

∴∠AOF＝∠ABD，

∵∠ABD＝∠PAD，

∴∠AOF＝∠PAD；

（3）解：延长OF交AD于点G，

∵OA＝OD，∠AOG＝∠DOG，

∴OG⊥AD，

∵tan∠PAD＝，∠AOF＝∠PAD，

∴tan∠AOF＝，

在Rt△AOG中，AO＝，

设AG＝x，

∴AG2+OG2＝AO2，

x2+（3x）2＝（）2，

解得：x＝，

∴AG＝，OG＝，

∵∠FAD＝45°，OG⊥AD，

∴∠AFG＝∠FAD＝45°，

∴FG＝AG＝，

∴OF＝OG﹣FG＝．