题目内容
 如图某海滨浴场的岸边AC可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,救生员没有从A处游向B处,而是沿岸边自A处跑到距离B处最近的C处,然后从C处游向B处.已知∠BAC=45°,AC=300米,救生员在岸边行进速度为6米/秒,在海中行进的速度为2米/秒.请分析救生员的路线选择是否正确.
如图某海滨浴场的岸边AC可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,救生员没有从A处游向B处,而是沿岸边自A处跑到距离B处最近的C处,然后从C处游向B处.已知∠BAC=45°,AC=300米,救生员在岸边行进速度为6米/秒,在海中行进的速度为2米/秒.请分析救生员的路线选择是否正确.分析:分别求得两个路线所用的时间,然后比较后即可得到答案.
解答:解:∵在Rt△ABC中,AC=300,∠BAC=45°,
∴BC=AC=300米,AB=
AC=300
米;
∵救生员在岸边行进速度为6米/秒,在海中行进的速度为2米/秒.
∴从A到B所用时间为:300
÷2=150
秒,
从A到C到B所用时间为:300÷6+300÷2=200秒,
∵200<150
∴救生员选择的路线正确.
∴BC=AC=300米,AB=
| 2 |
| 2 |
∵救生员在岸边行进速度为6米/秒,在海中行进的速度为2米/秒.
∴从A到B所用时间为:300
| 2 |
| 2 |
从A到C到B所用时间为:300÷6+300÷2=200秒,
∵200<150
| 2 |
∴救生员选择的路线正确.
点评:本题考查了勾股定理的应用,解题的关键是从实际问题中整理出直角三角形并正确的利用勾股定理求斜边的长.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
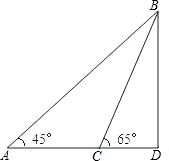 岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.
岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.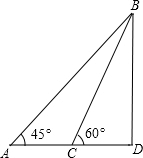 某海滨浴场的沿岸可以看作直线,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的D点,再跳入海中游到B点救助;若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=60°,且每位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.请你通过计算说明两位救生员谁先到达点B?
某海滨浴场的沿岸可以看作直线,如图所示,1号救生员在岸边的A点看到海中的B点有人求救,便立即向前跑300米到离B点最近的D点,再跳入海中游到B点救助;若2号救生员从A跑到C,再跳入海中游到B点救助,且∠BCD=60°,且每位救生员在岸上跑步的速度都是6米/秒,在水中游泳的速度都是2米/秒,∠BAD=45°.请你通过计算说明两位救生员谁先到达点B? 如图某海滨浴场的岸边AC可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,救生员没有从A处游向B处,而是沿岸边自A处跑到距离B处最近的C处,然后从C处游向B处.已知∠BAC=45°,AC=300米,救生员在岸边行进速度为6米/秒,在海中行进的速度为2米/秒.请分析救生员的路线选择是否正确.
如图某海滨浴场的岸边AC可近似地看成直线,位于岸边A处的救生员发现海中B处有人求救,救生员没有从A处游向B处,而是沿岸边自A处跑到距离B处最近的C处,然后从C处游向B处.已知∠BAC=45°,AC=300米,救生员在岸边行进速度为6米/秒,在海中行进的速度为2米/秒.请分析救生员的路线选择是否正确.