��Ŀ����
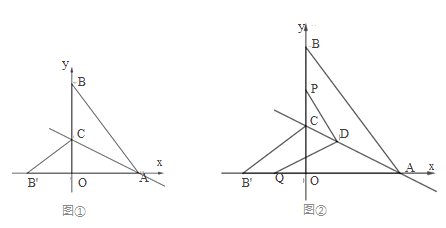
����Ŀ�����磬��ƽ��ֱ������ϵ�У���![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ���ϣ���ֱ��
���ϣ���ֱ��![]() .��
.��![]() ����ֱ��
����ֱ��![]() �ĶԳƵ�
�ĶԳƵ�![]() �պ���
�պ���![]() ���ϣ�����
���ϣ�����![]() .
.
��1��д��һ��![]() �����꣬�����ֱ��
�����꣬�����ֱ��![]() ��Ӧ�ĺ�������ʽ��
��Ӧ�ĺ�������ʽ��
��2����![]() ���߶�
���߶�![]() �ϣ�����
�ϣ�����![]() ��
��![]() ��
��![]() ����
����![]() �ǵ���ֱ��������ʱ�����
�ǵ���ֱ��������ʱ�����![]() ���ꣻ
���ꣻ
��3����ͼ�ڣ��ڣ�2���������£���![]() �ӵ�
�ӵ�![]() ������ÿ��2����λ���ȵ��ٶ���ԭ��
������ÿ��2����λ���ȵ��ٶ���ԭ��![]() �˶��������
�˶��������![]() ʱֹͣ�˶�������
ʱֹͣ�˶�������![]() ����
����![]() ��
��![]() �Ĵ��ߣ���
�Ĵ��ߣ���![]() ���ڵ�
���ڵ�![]() ���ʵ�
���ʵ�![]() �˶�����ʱ
�˶�����ʱ![]() �ǵ���������.
�ǵ���������.
���𰸡���1��![]() ��
��![]() ��2����
��2����![]() ����Ϊ
����Ϊ![]() ����3����
����3����![]() �˶�ʱ��Ϊ1���
�˶�ʱ��Ϊ1���![]() ���3.75��.
���3.75��.
��������
��1���ɹ��ɶ������AB=10���������A![]() =10���Ӷ������
=10���Ӷ������![]() ����C��0��m������ֱ��������
����C��0��m������ֱ��������![]() �У����ù��ɶ��������m��ֵ���Ӷ�ȷ����C�����꣬�����ô���ϵ�������AC�Ľ���ʽ���ɣ�
�У����ù��ɶ��������m��ֵ���Ӷ�ȷ����C�����꣬�����ô���ϵ�������AC�Ľ���ʽ���ɣ�
��2����![]() ��ֱƽ��
��ֱƽ��![]() ��֤
��֤![]() ������
������![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ��֤��
��֤��![]() �ɵ�DE=DF����D��a��a������
�ɵ�DE=DF����D��a��a������![]() ��⼴�ɣ�
��⼴�ɣ�
��3��������������ٵ�![]() ʱ���ڵ�
ʱ���ڵ�![]() ʱ���۵�
ʱ���۵�![]() ʱ���������ۼ��ɵý⣺
ʱ���������ۼ��ɵý⣺
��1��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��![]() ����ֱ��
����ֱ��![]() �ĶԳƣ�
�ĶԳƣ�
![]() ��ֱƽ��
��ֱƽ��![]() ��
��
![]() ��
��
![]() ��
��
���![]() ����Ϊ
����Ϊ![]() ����
����![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��![]() ��
��
![]() ��
��
![]()
![]() ��
��
![]() ��
��![]() ����Ϊ
����Ϊ![]() .
.
![]() ��ֱ��
��ֱ��![]() ��Ӧ�ĺ�������ʽΪ
��Ӧ�ĺ�������ʽΪ![]() ��
��
��![]() ���룬
���룬
��![]() ��
��
���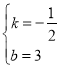 ��
��
![]() ֱ��
ֱ��![]() ��Ӧ�ĺ�����ϵ��Ϊ
��Ӧ�ĺ�����ϵ��Ϊ![]() ��
��
��2��![]() ��ֱƽ��
��ֱƽ��![]() ��
��
![]() ��
��
![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�
![]()
����![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.
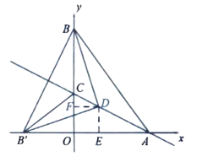
![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ���
���![]() ����Ϊ
����Ϊ![]() ��
��
�ѵ�![]() ����
����![]() ��
��
��![]()
![]() ��
��
![]() ��
��![]() ����Ϊ
����Ϊ![]() ��
��
��3��ͬ��2���ɵ�![]()
��![]()
![]()
![]()
�ٵ�![]() ʱ��
ʱ��
![]() �ᣬ
�ᣬ
![]()
![]()
![]()
![]() ��
��![]() �˶�ʱ��Ϊ1��.
�˶�ʱ��Ϊ1��.
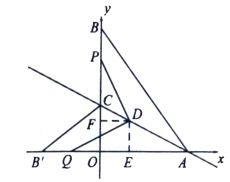
�ڵ�![]() ʱ��
ʱ��
![]()
![]()
![]() ��
��
![]()
![]()
![]() ��
��![]() �˶�ʱ��Ϊ
�˶�ʱ��Ϊ![]() ��.
��.
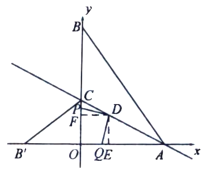
�۵�![]() ʱ��
ʱ��
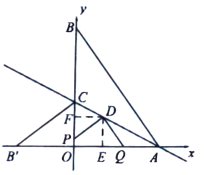
��![]() ����
����![]()
![]() ��
��![]() ��
��![]() ��
��
![]()
![]()
![]()
![]()
![]() ��
��![]() �˶�ʱ��Ϊ3.75��.
�˶�ʱ��Ϊ3.75��.
������������![]() �˶�ʱ��Ϊ1���
�˶�ʱ��Ϊ1���![]() ���3.75��.
���3.75��.

 ������ϵ�д�
������ϵ�д�