题目内容
已知a、b、c、d均为非负整数,且ac+bd+ad+bc=2003,求a+b+c+d.
答案:
解析:
解析:
|
因为ac+bd+ad+bc=(ac+ad)+(bd+bc)=a(c+d)+b(c+d)=(a+b)(c+d)=2003,故a+b=1,c+d=2003或a+b=2003,c+d=1,故a+b+c+d=2004. |

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
已知m是质数,x、y均为整数,则方程|x+y|+
=m的解的个数是( )
| x-y |
| A、2 | B、4 | C、5 | D、无数个 |
 27、已知:如图,△ABC和△DBE均为等腰直角三角形.
27、已知:如图,△ABC和△DBE均为等腰直角三角形.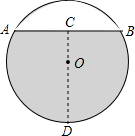 如图所示是一个水平放置的圆柱形水管的横截面,已知水平面高CD和水面宽AB均为80cm,则水管横截面圆的半径为
如图所示是一个水平放置的圆柱形水管的横截面,已知水平面高CD和水面宽AB均为80cm,则水管横截面圆的半径为