题目内容
计算:
(1)-32-23÷ ×3;
×3;
(2)(1- +
+ )×(-48);
)×(-48);
(3) ;
;
(4)先化简,再求值:(2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3),其中x=1,y=2,z=-3.
解:
(1)-32-23÷ ×3=-9-8×3×3=-81;
×3=-9-8×3×3=-81;
(2)(1- +
+ )×(-48)=1×(-48)-
)×(-48)=1×(-48)- ×(-48)+
×(-48)+ ×(-48)=-48+8-36=-76;
×(-48)=-48+8-36=-76;
(3)原式=( -
- )m+(-
)m+(- -
- )n=
)n=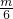 -
- ;
;
(4)原式=2x3-xyz-2x3+2y3-2xyz+xyz-2y3=-2xyz,
当x=1,y=2,z=-3时,原式=-2×1×2×(-3)=12.
分析:(1)先算乘方,后算乘除;
(2)用分配律解答;
(3)合并同类项;
(4)去括号,合并同类项.
点评:此题考查了有理数会和运算,乘法分配律,合并同类项等知识,内容较多,仔细解答.
(1)-32-23÷
 ×3=-9-8×3×3=-81;
×3=-9-8×3×3=-81;(2)(1-
 +
+ )×(-48)=1×(-48)-
)×(-48)=1×(-48)- ×(-48)+
×(-48)+ ×(-48)=-48+8-36=-76;
×(-48)=-48+8-36=-76;(3)原式=(
 -
- )m+(-
)m+(- -
- )n=
)n=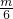 -
- ;
;(4)原式=2x3-xyz-2x3+2y3-2xyz+xyz-2y3=-2xyz,
当x=1,y=2,z=-3时,原式=-2×1×2×(-3)=12.
分析:(1)先算乘方,后算乘除;
(2)用分配律解答;
(3)合并同类项;
(4)去括号,合并同类项.
点评:此题考查了有理数会和运算,乘法分配律,合并同类项等知识,内容较多,仔细解答.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案
相关题目