Question

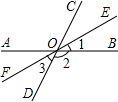
直线AB、CD相交于点O，OE平分∠AOD，∠FOC=90°，∠1=40°，求∠2与∠3的度数。（10分）

Answer 1

∠2=65°，∠3=50°

解析考点：对顶角、邻补角；角平分线的定义。
分析：由已知∠FOC=90°，∠1=40°结合平角的定义，可得∠3的度数，又因为∠3与∠AOD互为邻补角，可求出∠AOD的度数，又由OE平分∠AOD可求出∠2。
解答：
∵∠FOC=90°，∠1=40°，AB为直线，
∴∠3+∠FOC+∠1=180°，
∴∠3=180°-90°-40°=50°。
∠3与∠AOD互补，
∴∠AOD=180°-∠3=130°，
∵OE平分∠AOD，
∴∠2=1/2∠AOD=65°。
点评：本题主要考查邻补角的概念以及角平分线的定义。