Question

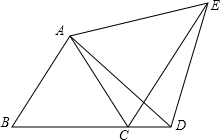
将边长分别为2、4、6的三个正三角形按如图方式排列，A、B、C、D在同一直线上，则图中阴影部分的面积的和为______．

Answer 1

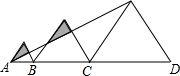
如图，在三个正三角形中，∠ABE=∠BCF=∠CDG=60°，
∴BE∥CF∥DG，
∴

CF

DG

=

AC

AD

，
即

CF

6

=

2+4

2+4+6

，
解得CF=3，
∴第二个三角形中的阴影部分三角形的底边长为4-3=1，
同理

BE

CF

=

AB

AC

，
即

BE

3

=

2

2+4

，
解得BE=1，
边长为4的等边三角形的高为：4×

3

2

=2

3

，
∴阴影部分的面积的和=△BEH的面积+第二个等边三角形中的阴影部分的面积，
即

1

2

×1×2

3

=

3

．
故答案为：

3

．