题目内容
如图所示，某船上午11时30分在A处观测海岛B在北偏东60°方向，该船以每小时10海里的速度航行
到C处，再观测海岛B在北偏东30°方向，又以同样的速度继续航行到D处，再观测海岛在北偏西30°方向，当轮船到达C处时恰好与海岛B相距20海里，请你确定轮船到达C
处和D处的时间。
解：∵∠BAD=30°, ∠BCD=∠BDC=∠CBD=60°
∴△BCD为等边三角形
在△ABD中，∠BAD=30°, ∠BDC=60°
∴∠ABD=90°，即△ABD为直角三角形。
∵BC=20海里，
∴CD=BD=20海里。
又∵BD=
AD
∴AD=40海里
∴AC=AD-CD=20海里
练习册系列答案
相关题目
下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差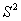
：
| 甲 | 乙 | 丙 | 丁 | |
|
| 175 | 173 | 175 | 174 |
| 方差 | 3.5 | 3.5 | 12.5 | 15 |
平均数x（cm）根据表中数据，要从中选择一名成绩好又发挥稳定的运动员参加比赛，应该选择
A．甲 B．乙 C．丙 D．丁
∠C，则三角形是（ ）
