Question

【题目】已知的周长为28，过点分别作，交直线于点，，交直线于点，若，，则的长为____．

Answer 1

【答案】或

【解析】

根据∠A为锐角或∠D为锐角分情况进行讨论，由ABCD的周长为28，DE⊥BC，DF⊥AB，垂足分别为E、F，且DE=3，DF=4，构造方程求解即可求得答案．

对于平行四边形ABCD有两种情况：

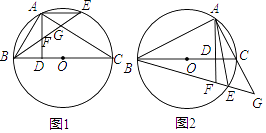
当∠A为锐角时，如图1，

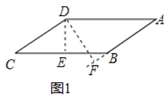
设BC=a，AB=b，

∵平行四边形ABCD，DE⊥AB，DF⊥BC，

∴AB×DE=BC×DF，AB=CD，BC=DA，

又∵DE=3，DF=4，

∴3a=4b，

∵平行四边形ABCD的周长为28，

∴2（a+b）=28，

∴a+b=14，

则，

解得：，

∴BC=8，AB=6，

∴AB=CD=6，AD=BC=8，

∴在Rt△CDE中，CE=3，

∴BE=BC-CE=8-3，

∴在Rt△ADF中，AF=4，

∵F点在AB的延长线上，

∴BF=AF-AB=4-6，

∴BE+BF=（8-3）+（4-6）=2+；

当∠D为锐角时，如图2，

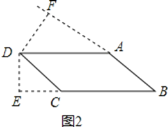
设BC=a，AB=b，

∵平行四边形ABCD，DE⊥BC，DF⊥AB，

∴AB×DF=BC×DE，AB=CD，BC=DA，

又∵DE=3，DF=4，

∴3a=4b，

∵平行四边形ABCD的周长为28，

∴2（a+b）=28，

∴a+b=14，

解方程组，

解得：，

∴BC=8，AB=6，

∴AB=CD=6，AD=BC=8，

∴在Rt△CDE中，CE=3，

∴BE=BC+CE=8+3，

∴在Rt△ADF中，AF=4，

∵F点在AB的延长线上，

∴BF=AF+AB=4+6，

∴BE+BF=（8+3）+（4+6）=14+7，

故答案为：2+或14+7．