题目内容
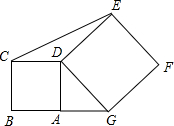 如图,在线段BG上,四边形ABCD和四边形DEFG都是正方形,面积分别是7cm2和11cm2,则△CDE的面积为
如图,在线段BG上,四边形ABCD和四边形DEFG都是正方形,面积分别是7cm2和11cm2,则△CDE的面积为分析:根据三角形的面积公式,已知边CD的长,求出CD边上的高即可.
过E作EH⊥CD,易证△ADG与△HDE全等,求得EH,进而求△CDE的面积.
过E作EH⊥CD,易证△ADG与△HDE全等,求得EH,进而求△CDE的面积.
解答: 解:过E作EH⊥CD.
解:过E作EH⊥CD.
∵∠ADG+∠GDH=∠EDH+∠GDH,
∴∠ADG=∠EDH.
又∵DG=DE,∠DAG=∠DHE.
∴△ADG≌△HDE.
∴HE=AG.
∵四边形ABCD和四边形DEFG都是正方形,面积分别是7cm2和11cm2.即AD2=7,DG2=11.
∴在直角△ADG中,AG=
=
=2.
∴EH=AG=2.
∴△CDE的面积为
CD•EH=
×
×2=
(cm2).
 解:过E作EH⊥CD.
解:过E作EH⊥CD.∵∠ADG+∠GDH=∠EDH+∠GDH,
∴∠ADG=∠EDH.
又∵DG=DE,∠DAG=∠DHE.
∴△ADG≌△HDE.
∴HE=AG.
∵四边形ABCD和四边形DEFG都是正方形,面积分别是7cm2和11cm2.即AD2=7,DG2=11.
∴在直角△ADG中,AG=
| DG2-AD2 |
| 11-7 |
∴EH=AG=2.
∴△CDE的面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 7 |
点评:正确作出辅助线,构造全等三角形是解决本题的关键.

练习册系列答案
相关题目
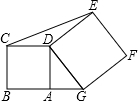 如图,点A在线段BG上,四边形ABCD和四边形DEFG都是正方形,面积分别是5cm2和9cm2,则△CDE的面积为
如图,点A在线段BG上,四边形ABCD和四边形DEFG都是正方形,面积分别是5cm2和9cm2,则△CDE的面积为
 ;
; =
=


 .
.

 ;
; =
=


 .
.
 如图,在线段BG上,四边形ABCD和四边形DEFG都是正方形,面积分别是7cm2和11cm2,则△CDE的面积为________cm2.
如图,在线段BG上,四边形ABCD和四边形DEFG都是正方形,面积分别是7cm2和11cm2,则△CDE的面积为________cm2.