题目内容
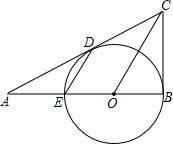 如图,CB、CD是⊙O的切线,切点分别为B、D,CD的延长线与⊙O的直径BE的延长线交于A点,连OC,ED.探索OC与ED的位置关系,并加以证明.
如图,CB、CD是⊙O的切线,切点分别为B、D,CD的延长线与⊙O的直径BE的延长线交于A点,连OC,ED.探索OC与ED的位置关系,并加以证明.
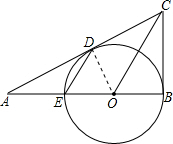 解:OC∥ED;理由如下:
解:OC∥ED;理由如下:连接OD.
∵BC、CD是⊙O的切线,
∴∠CBO=∠CDO=90°.
∵OD=OB,CO=CO,
∴Rt△COB≌Rt△COD(HL).
∴∠COD=∠COB.
又∵OD=OE,
∴∠EDO=∠DEO(等边对等角).
∵∠DEO=
 ∠DOB(同弧所对的圆周角是所对的圆心角的一半),
∠DOB(同弧所对的圆周角是所对的圆心角的一半),∴∠DEO=∠COB(等量代换).
∴OC∥ED(同位角相等,两直线平行).
分析:连接OD,证△COD≌△COB,则∠COD=∠COB;又∠DOB是等腰△ODE的外角,则∠DOB=2∠DEB,由此可证得∠COB=∠DEB;同位角相等,则DE∥OC.
点评:本题考查了圆周角定理、切线的性质.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
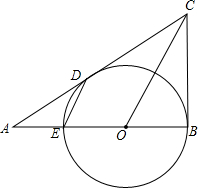 如图,CB、CD是⊙O的切线,切点分别为B、D.CD的延长线与⊙O的直径BE的延长线交于A点,连接OC,ED.
如图,CB、CD是⊙O的切线,切点分别为B、D.CD的延长线与⊙O的直径BE的延长线交于A点,连接OC,ED.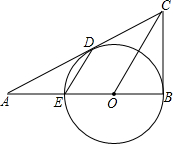 如图,CB、CD是⊙O的切线,切点分别为B、D,CD的延长线与⊙O的直径BE的延长线交于A点,连OC,ED.探索OC与ED的位置关系,并加以证明.
如图,CB、CD是⊙O的切线,切点分别为B、D,CD的延长线与⊙O的直径BE的延长线交于A点,连OC,ED.探索OC与ED的位置关系,并加以证明. 如图,CB、CD是⊙O的切线,切点分别为B、D.CD的延长线与⊙O的直径BE的延长线交于A点,连接OC,ED.
如图,CB、CD是⊙O的切线,切点分别为B、D.CD的延长线与⊙O的直径BE的延长线交于A点,连接OC,ED.
