题目内容
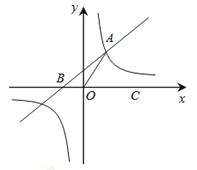
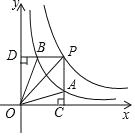
【题目】函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图,点P是y=
在第一象限内的图象如图,点P是y=![]() 的图象上一动点,PC⊥x轴于点C,交y=
的图象上一动点,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B.下面结论:
的图象于点B.下面结论:
①PA与PB始终相等;②△OBP与△OAP的面积始终相等;
③四边形PAOB的面积不变;④PABD=PBAC.
其中一定正确的是_____(把你认为正确结论的序号都填上)
【答案】②③④
【解析】
根据反比例函数的图象和性质,特别是根据反比例函数k的几何意义,对四个选项逐一进行分析,即可得出正确答案.
解:∵A、B是反比函数y=![]() 上的点,
上的点,
∴S△OBD=S△OAC=![]() ,
,
∵点P在y=![]() 上,
上,
∴S△PDO=S△POC=![]() ,
,
∴S△POB=S△POA=1,故②正确,
∵当P的横纵坐标相等时PA=PB,故①错误;
∴S四边形PAOB=S△PBO+S△POA=3,故③正确;
连接OP,
∵![]() =3,
=3,
∴AC=![]() PC,PA=
PC,PA=![]() PC,
PC,
∴![]() =2,
=2,
同理可得![]() =2,
=2,
∴![]() =
=![]() ,即PABD=PBAC故④正确.
,即PABD=PBAC故④正确.

故答案为:②③④.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
【题目】为了了解学生学习的环境(教室),研究人员对某校一间(坐满学生、门窗关闭)教室中的![]() 的总量进行检测,得到的部分数据如下:
的总量进行检测,得到的部分数据如下:
教室连续使用时间 |
|
|
|
|
|
|
|
|
|
|
|
经研究发现,该教室空气中![]() 总量
总量![]()
![]() 是教室连使用时间
是教室连使用时间![]()
![]() 的一次函数.
的一次函数.
(1)请直接写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)根据有关资料推算,当该教室空气中![]() 总量达到
总量达到![]() 时,学生将会稍感不适,则该教室连续使用__________
时,学生将会稍感不适,则该教室连续使用__________![]() 学生将会开始稍感不适.
学生将会开始稍感不适.
(3)如果该教室在连续使用![]() 分钟时开门通风,在学生全部离开教室的情况下,
分钟时开门通风,在学生全部离开教室的情况下,![]() 分钟可将教室空气中
分钟可将教室空气中![]() 的总量减少到
的总量减少到![]() ,求开门通风时教室空气中
,求开门通风时教室空气中![]() 平均每分钟减少多少立方米?
平均每分钟减少多少立方米?