题目内容
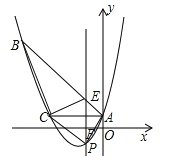
【题目】如图，已知抛物线
经过△ABC的三个顶点，其中点A（0，1），点B（﹣9，10），AC∥x轴，点P是直线AC下方抛物线上的动点．
（1）求抛物线的解析式；
（2）过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F，当四边形AECP的面积最大时，求点P的坐标；
（3）当点P为抛物线的顶点时，在直线AC上是否存在点Q，使得以C、P、Q为顶点的三角形与△ABC相似，若存在，求出点Q的坐标，若不存在，请说明理由．
【答案】（1）
；（2）P（
，
）；（3）Q（﹣4，1），Q（3，1）．
【解析】
试题分析：（1）用待定系数法求出抛物线解析式即可；
（2）设点P（m，
），表示出PE=
，再用S四边形AECP=S△AEC+S△APC=
AC×PE，建立函数关系式，求出极值即可；
（3）先判断出PF=CF，再得到∠PCF=∠EAF，以C、P、Q为顶点的三角形与△ABC相似，分两种情况计算即可．
试题解析：（1）∵点A（0，1）．B（﹣9，10）在抛物线上，∴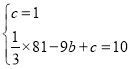
，∴
，∴抛物线的解析式为；
（2）∵AC∥x轴，A（0，1）
∴
=1，∴
=6，
=0，∴点C的坐标（﹣6，1），∵点A（0，1）．B（﹣9，10），∴直线AB的解析式为y=﹣x+1，设点P（m，），∴E（m，﹣m+1），∴PE=﹣m+1﹣（）=，∵AC⊥EP，AC=6，∴S四边形AECP=S△AEC+S△APC=AC×EF+AC×PF=AC×（EF+PF）
=AC×PE=×6×（）=
=
∵﹣6＜m＜0，∴当m=﹣
时，四边形AECP的面积的最大值是
，此时点P（，）．
（3）∵=
，∴P（﹣3，﹣2），∴PF=yF﹣yP=3，CF=xF﹣xC=3，∴PF=CF，∴∠PCF=45°；
同理可得：∠EAF=45°，∴∠PCF=∠EAF，∴在直线AC上存在满足条件的Q，设Q（t，1）且AB=
，AC=6，CP=
．∵以C、P、Q为顶点的三角形与△ABC相似，①当△CPQ∽△ABC时，∴
，∴
，∴t=﹣4，∴Q（﹣4，1）；
②当△CQP∽△ABC时，∴
，∴
，∴t=3，∴Q（3，1）．
综上所述：Q（﹣4，1），Q（3，1）．
