题目内容
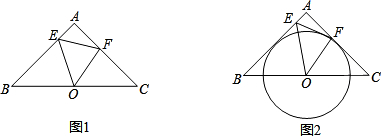
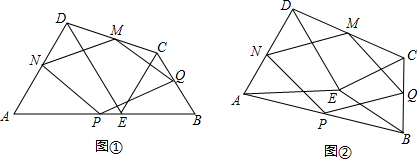
如图①,分别以AE、BE为边在AB的同侧作等边△ADE和等边△BCE,AB、BC、CD、DA的中点分别为P、Q、M、N.(1)判断四边形PQMN的形状,并说明你的理由;
(2)如图②,将△BCE绕着点E顺时针旋转,其它条件不变,判断四边形PQMN的形状,并说明你的理由.
分析:(1)易证∴△AEC≌△DEB得AC=DB,根据AB、BC、CD、DA的中点分别为P、Q、M、N,可证PQ=MN=
AC,PQ∥MN∥AC,四边形PQMN为平行四边形,邻边相等的平行四边形可以判定为菱形;
(2)易证∴△AEC≌△DEB得AC=DB,根据AB、BC、CD、DA的中点分别为P、Q、M、N,可证PQ=MN=
AC,PQ∥MN∥AC,四边形PQMN为平行四边形,邻边相等的平行四边形可以判定为菱形.
| 1 |
| 2 |
(2)易证∴△AEC≌△DEB得AC=DB,根据AB、BC、CD、DA的中点分别为P、Q、M、N,可证PQ=MN=
| 1 |
| 2 |
解答: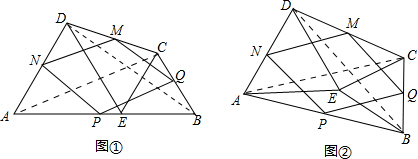 解:
解:
(1)四边形PQMN为菱形.
证明:连接AC、BD,
∵AE=DE,∠AEC=∠DEB,CE=BE,
∴△AEC≌△DEB,
∴AC=DB,
∵AB、BC、CD、DA的中点分别为P、Q、M、N,
∴PQ=MN=
AC,PQ∥MN∥AC,
∴四边形PQMN为平行四边形,
同理MQ=
BD,
∴MQ=PQ,
∴四边形PQMN为菱形;
(2)四边形PQMN仍为菱形.
证明:连接AC、BD,
∵AE=DE,∠AEC=∠DEB,CE=BE,
∴△AEC≌△DEB,
∴AC=DB,
∵AB、BC、CD、DA的中点分别为P、Q、M、N,
∴PQ=MN=
AC,PQ∥MN∥AC,
∴四边形PQMN为平行四边形,
同理MQ=
BD,
∴MQ=PQ,
∴四边形PQMN为菱形.
 解:
解:(1)四边形PQMN为菱形.
证明:连接AC、BD,
∵AE=DE,∠AEC=∠DEB,CE=BE,
∴△AEC≌△DEB,
∴AC=DB,
∵AB、BC、CD、DA的中点分别为P、Q、M、N,
∴PQ=MN=
| 1 |
| 2 |
∴四边形PQMN为平行四边形,
同理MQ=
| 1 |
| 2 |
∴MQ=PQ,
∴四边形PQMN为菱形;
(2)四边形PQMN仍为菱形.
证明:连接AC、BD,
∵AE=DE,∠AEC=∠DEB,CE=BE,
∴△AEC≌△DEB,
∴AC=DB,
∵AB、BC、CD、DA的中点分别为P、Q、M、N,
∴PQ=MN=
| 1 |
| 2 |
∴四边形PQMN为平行四边形,
同理MQ=
| 1 |
| 2 |
∴MQ=PQ,
∴四边形PQMN为菱形.
点评:本题考查了全等三角形的证明,全等三角形对应边相等的性质,菱形的判定,平行四边形的判定,本题中求证AC=BD是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目