Question

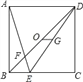
【题目】如图，正方形ABCD中，点E在边BC上，且CE=2BE．连接BD、DE、AE，且AE交BD于F，OG为△BDE的中位线．下列结论：①OG⊥CD；②AB=5OG；③；④BF=OF；⑤，其中正确结论的个数是（　　）

A. 2 B. 3 C. 4 D. 5

Answer 1

【答案】B

【解析】分析：①由正方形的性质与为的中位线，即可证得
②由为的中位线的性质与 可求得
③由相似三角形的面积比等于相似比的平方与等高等底三角形的面积相等，即可求得
④由相似三角形的对应边成比例，易求得
⑤首先过点B作，首先设，由相似三角形的性质与勾股定理，可求得BF与FH的长，继而求得答案．

详解：①∵四边形ABCD是正方形，
∴
即
∵为的中位线，
∴OG∥BC，
∴故正确；
②∵为的中位线，
∴
∵
∴
∴ 故错误；
③∵OG∥BC，
∴
∴
∵
∴ 故错误；
④∵
∴
∵BC∥AD，
∴

故正确；

⑤过点B作，

∵
∴
∴
∴
∵设 则
在中

∴

在中，

∴ 故正确．
故选B．