Question

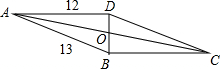
已知：如图，在平行四边形ABCD中，连接对角线BD，作AE⊥BD于E，CF⊥BD于F，
（1）求证：△AED≌△CFB；
（2）若∠ABC=75°，∠ADB=30°，AE=3，求平行四边形ABCD的周长．

Answer 1

（1）证明：∵四边形ABCD是平行四边形，
∴AD=BC，AD∥BC，
∴∠ADE=∠CBF，
又∵AE⊥BD于E，CF⊥BD于F，
∴∠AED=∠CFB=90°，
在△AED和△CFB中，

AD=BC ∠ADE=∠CBF ∠AED=∠CFB

，
∴△AED≌△CFB（AAS）；

（2）在Rt△AED中，
∵∠ADE=30°，AE=3，
∴AD=2AE=2×3=6，
∵∠ABC=75°，∠ADB=∠CBD=30°
∴∠ABE=45°，
在Rt△ABE中，
∵

AE

AB

=sin45°，
∴AB=

AE

sin45°

=3

2

，
∴平行四边形ABCD的周长l=2（AB+AD）=2×（6+3

2

）=12+6

2

．