题目内容
已知∠α是△ABC的一个锐角，且AB=3，BC=4，AC=5，计算：25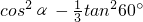
．
解：∵AB=3，BC=4，AC=5，
∴AB2+BC2=AC2，
∴∠B=90°，
当∠α=∠A时，cosα=
=
，
原式=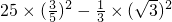
=8，
当∠α=∠C时，cosα=
=
，
原式=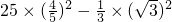
=15．
分析：先根据AB=3，BC=4，AC=5，得出AB2+BC2=AC2，∠B=90°，再分当∠α=∠A时，cosα==，当∠α=∠C时，cosα==两种情况代入计算即可．
点评：此题考查了解直角三角形，要掌握锐角三角函数的概念和特殊角的三角函数值，关键是根据已知条件证出△ABC是直角三角形，要注意分两种情况讨论．
∴AB2+BC2=AC2，
∴∠B=90°，
当∠α=∠A时，cosα=
=，原式=
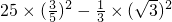
=8，
当∠α=∠C时，cosα=
=，原式=
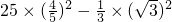
=15．
分析：先根据AB=3，BC=4，AC=5，得出AB2+BC2=AC2，∠B=90°，再分当∠α=∠A时，cosα=
=，当∠α=∠C时，cosα==两种情况代入计算即可．点评：此题考查了解直角三角形，要掌握锐角三角函数的概念和特殊角的三角函数值，关键是根据已知条件证出△ABC是直角三角形，要注意分两种情况讨论．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
已知α，β是△ABC的两个角，且sinα，tanβ是方程2x2-3x+1=0的两根，则△ABC是（ ）
| A、锐角三角形 | B、直角三角形或钝角三角形 | C、钝角三角形 | D、等边三角形 |
9、如图，已知AD是△ABC的角平分线，CE⊥AD，垂足O，CE交AB于E，则下列命题：①AE=AC，②CO=OE，③∠AEO=∠ACO，④∠B=∠ECB．其中正确的是（ ）已知O是△ABC的外心，∠ABC=60°，AC=4，则△ABC外接圆的半径是（ ）
A、
| ||||
B、2
| ||||
C、
| ||||
D、
|
F⊥AB于F，且CE=CF．
如图，已知BE是△ABC的高，AE=BE，