题目内容
【题目】
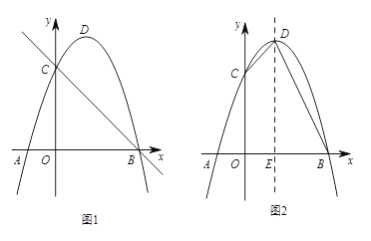
如图1,抛物线![]() 与x轴交于点
与x轴交于点![]() 、点
、点![]() (点
(点![]() 在点
在点![]() 左侧),与
左侧),与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为顶点,已知点
为顶点,已知点![]() 、点
、点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() 。
。
(1)求抛物线的解析式;
(2)在直线![]() 上方的抛物线上找一点
上方的抛物线上找一点![]() ,使
,使![]() 的面积最大,求
的面积最大,求![]() 点坐标;
点坐标;
(3)如图2,连结![]() 、
、![]() ,抛物线的对称轴与x轴交于点
,抛物线的对称轴与x轴交于点![]() 。过抛物线上一点
。过抛物线上一点![]() 作
作![]() ,交直线
,交直线![]() 于点
于点![]() ,求当
,求当![]() 时点
时点![]() 的坐标。
的坐标。
【答案】(1)抛物线的表达式为:![]() ;
;
(2)当![]() 时,S△BCD取最大值,此时P(
时,S△BCD取最大值,此时P(![]() ,
,![]() );
);
(3)点M坐标为(![]() ,
,![]() )或(
)或(![]() ).
).
【解析】试题分析:(1)把点A(-1,0)和点B(3,0)的坐标代入所给抛物线可得a、b的值,进而得到该抛物线的解析式;(2) )由题意设P(![]() ),过点P作x轴的垂线,交直线BC于点Q,再求得直线CB解析式,可得点Q的坐标,再求得PQ的长,利用S△BCD=
),过点P作x轴的垂线,交直线BC于点Q,再求得直线CB解析式,可得点Q的坐标,再求得PQ的长,利用S△BCD=![]() 得出以S、x为变量的二次函数模型,利用二次函数的性质求得x的值,即可得点P的坐标.(3)先求得点C,点E和顶点的坐标,再分当点M在对称轴右侧时和当点M在对称轴左侧时两种情况求解即可.
得出以S、x为变量的二次函数模型,利用二次函数的性质求得x的值,即可得点P的坐标.(3)先求得点C,点E和顶点的坐标,再分当点M在对称轴右侧时和当点M在对称轴左侧时两种情况求解即可.
试题解析:
解:(1)将A(-1,0)、B(3,0)两点代入![]() 得:
得:
![]()
解得:![]()
∴抛物线的表达式为:![]()
(2)由题意设P(![]() ),过点P作x轴的垂线,交直线BC于点Q,
),过点P作x轴的垂线,交直线BC于点Q,
直线CB解析式:![]() , 则Q(
, 则Q(![]() )
)
∴PQ=![]()
S△BCD=![]()
∵![]() ,∴当
,∴当![]() 时,S△BCD取最大值,
时,S△BCD取最大值,
此时P(![]() )
)
(3)∵抛物线y=﹣(x﹣3)(x+1)=﹣x2+2x+3与与y轴交于点C,
∴C点坐标为(0,3),顶点(1,4),E(1,0)
∴tan∠BDE=![]()
(Ⅰ)当点M在对称轴右侧时.
i)若点N在射线CD上,
如图,过点N作y轴的垂线,垂足为G,过点M作GN的垂线,垂足为H,
则△CNG,△MNH均为等腰直角三角形,
∵∠CMN=∠BDE,∴tan∠CMN = tan∠BDE![]()
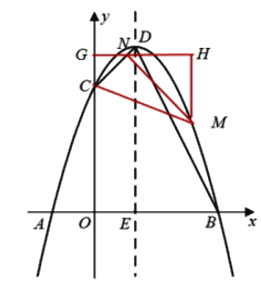
∴△CNG,△MNH相似比为1:2
设CG=a,则NG=a,NH=NH=2a,
∴M(3a,3+a-2a),即M(3a,3-a),
代入![]() 得:
得:
![]()
解得:![]()
此时M(![]() )
)
ii)若点N在射线DC上,
如图,过点N作x轴的垂线l,分别过点M、C作GN的垂线,垂足为H、G,
则△CNG,△MNH均为等腰直角三角形,
∵∠CMN=∠BDE,∴tan∠CMN = tan∠BDE![]()
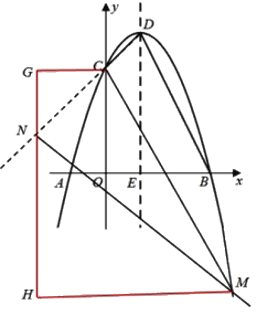
∴△CNG,△MNH相似比为1:2
设CG=a,则NG=a,NH=NH=2a,
∴M(a,3-a-2a),即M(a,3-3a),
代入![]() 得:
得:
![]()
解得:![]()
此时M(![]() )
)
(Ⅱ)当点M在对称轴左侧时.
∵∠CMN=∠BDE<45°,
∴∠MCN>45°,
而抛物线左侧任意一点K,都有∠KCN<45°,
∴点M不存在.
综上可知,点M坐标为(![]() ,
,![]() )或(
)或(![]() ).
).

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案