Question

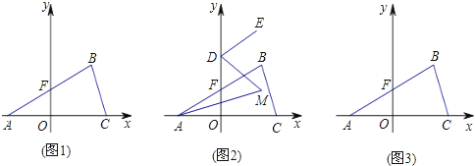
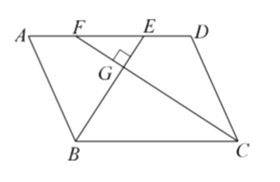
【题目】如图，在△ABC 中，∠A＝90°，AB＝AC，∠ABC 的角平分线交 AC 于 D，BD＝4 ，过点 C作 CE⊥BD 交 BD 的延长线于 E，则 CE 的长为（ ）

A.B.2 C.3 D.2

Answer 1

【答案】D

【解析】

延长CE与BA延长线交于点F，首先证明△BAD≌△CAF，根据全等三角形的性质得出BD=CF，再证明△BEF≌△BCF得出CE=EF，进而可得CE=BD，即可得出答案．

延长CE与BA相交于点F

∵∠BAC=90°，CE⊥BD

∴∠BAC=∠DEC

∵∠ADB=∠CDE

∴∠ABD=∠DCE

在△BAD和△CAF中

∴△BAD≌△CAF

∴BD=CF

∵BD平分∠ABC，CE⊥DB

∴∠FBE=∠CBE

在△BEF和△BCE中

∴△BEF≌△BCE

∴CE=CF

∴DB=2CE

即CE=BD=

故答案选择D．