题目内容
 已知两直线l1和l2相交于点A(2,1),且直线l2经过坐标原点,若OA=OB
已知两直线l1和l2相交于点A(2,1),且直线l2经过坐标原点,若OA=OB
(1)求l1和l2的函数关系式;
(2)求△OAB的面积.
解:(1)∵点A(2,1)
∴OA=
∵OA=OB
∴B(0,- )
)
设l1=kx+b,l2=k′x,则
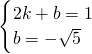 ,2k′=1
,2k′=1
∴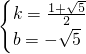 ,k′=
,k′=
∴l1= x-
x-
l2= x.
x.
(2)S△AOB=
 2
2 OB=
OB= ×2
×2
 =
= .
.
分析:(1)先求得B的坐标,利用待定系数法可分别求得l1和l2的函数关系式;
(2)S△AOB= ×点A的横坐标×OB,代入数值即可求解.
×点A的横坐标×OB,代入数值即可求解.
点评:主要考查了待定系数法求函数解析式,并会利用数形结合的方法求得坐标系中的特殊图形的面积.关键是要找到三角形的高和底,能灵活的运用各点的坐标表示.
∴OA=

∵OA=OB
∴B(0,-
 )
)设l1=kx+b,l2=k′x,则
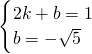 ,2k′=1
,2k′=1∴
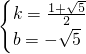 ,k′=
,k′=
∴l1=
 x-
x-
l2=
 x.
x.(2)S△AOB=

 2
2 OB=
OB= ×2
×2
 =
= .
.分析:(1)先求得B的坐标,利用待定系数法可分别求得l1和l2的函数关系式;
(2)S△AOB=
 ×点A的横坐标×OB,代入数值即可求解.
×点A的横坐标×OB,代入数值即可求解.点评:主要考查了待定系数法求函数解析式,并会利用数形结合的方法求得坐标系中的特殊图形的面积.关键是要找到三角形的高和底,能灵活的运用各点的坐标表示.

练习册系列答案
相关题目
 如图,已知两直线l1和l2相交于点A(4,3),且OA=OB,请分别求出两条直线对应的函数解析式.
如图,已知两直线l1和l2相交于点A(4,3),且OA=OB,请分别求出两条直线对应的函数解析式. 已知两直线l1和l2相交于点A(2,1),且直线l2经过坐标原点,若OA=OB
已知两直线l1和l2相交于点A(2,1),且直线l2经过坐标原点,若OA=OB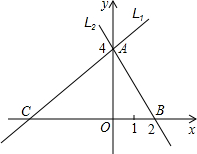 B两点,两直线相交于点A.
B两点,两直线相交于点A. 已知两直线L1和L2,直线L1的解析式是y=x-4,且直线L1与x轴交于点C,直线L2经过A、B两点,两直线相交于点A.
已知两直线L1和L2,直线L1的解析式是y=x-4,且直线L1与x轴交于点C,直线L2经过A、B两点,两直线相交于点A. B两点,两直线相交于点A.
B两点,两直线相交于点A.