Question

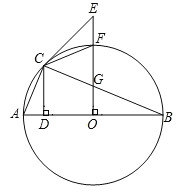
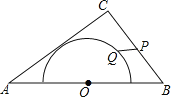
【题目】如图，在△ABC中，AB＝10，AC＝8，BC＝6，以边AB中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最大值与最小值的和是__．

Answer 1

【答案】9

【解析】

如图，设 O与AC相切于点E，连接OE，作⊥BC垂足为交 O于，此时垂线段最短，最小值为，求出，如图当在AB边上时，与B重合时，最大值=5+3=8，由此不难解决问题．

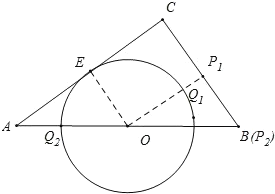
如图,设O与AC相切于点E,连接OE,作⊥BC垂足为交 O于，

此时垂线段最短, 最小值为，

∵AB=10，AC=8，BC=6，

∴，

∴∠C=90°，

∵∠=90°，

∴∥AC

∵AO=OB，

∴C=B，

∴=AC=4，

∴最小值为=1，

如图,当在AB边上时, 与B重合时, 经过圆心，经过圆心的弦最长，

最大值=5+3=8，

∴PQ长的最大值与最小值的和是9.

故答案为：9.