��Ŀ����
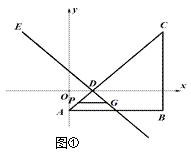
����Ŀ����ͼ�٣�����ֱ��������ABC�Ķ���A������Ϊ ![]() ��C������Ϊ
��C������Ϊ ![]() ��ֱ�Ƕ���B�ڵ������ޣ��߶�AC��x�ύ�ڵ�D.���߶�DC�Ƶ�D��ʱ����ת90����DE.
��ֱ�Ƕ���B�ڵ������ޣ��߶�AC��x�ύ�ڵ�D.���߶�DC�Ƶ�D��ʱ����ת90����DE.
��1��ֱ��д����B��D��E�����겢���ֱ��DE�Ľ���ʽ.
��2����ͼ�ڣ���P��ÿ��1����λ���ٶ����߶�AC�ӵ�A�˶�����C�Ĺ����У�����P����x��ƽ�е�ֱ��PG����ֱ��DE�ڵ�G�������DPG�����S���˶�ʱ��t�ĺ�����ϵʽ��������Ա���t��ȡֵ��Χ.
��3����ͼ�ۣ����FΪֱ��DE�ϵĵ㣬����AF��һ����M�ӵ�A���������߶�AF��ÿ��1����λ���ٶ��˶���F�������߶�FE��ÿ�� ![]() ����λ���ٶ��˶���E��ֹͣ.����F�������Ƕ���ʱ���Ƿ���ڵ�M�������˶���������ʱ���٣������ڣ��������F�����ꣻ�������ڣ���˵������.
����λ���ٶ��˶���E��ֹͣ.����F�������Ƕ���ʱ���Ƿ���ڵ�M�������˶���������ʱ���٣������ڣ��������F�����ꣻ�������ڣ���˵������.
���𰸡�
��1���⣺������ã�B(4,-1),D(1,0).E(-2,3)
��ֱ��DEΪ ![]()
![]()
��D(1,0).E(-2,3)�����
![]()
��֮�ã� ![]()
��ֱ��DEΪ�� ![]()
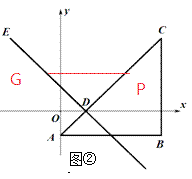
��2���⣺��Rt��ABC�У��� ![]()
![]() ��
��
�� ![]()
![]()
ͬ���ɵã� ![]()
�������֪�� ![]() ����DPG=��DAB=45��
����DPG=��DAB=45��
���DPGΪ����ֱ��������
![]()
�ٵ� ![]() ʱ
ʱ
�� ![]()
![]()
�ڵ� ![]() ʱ��
ʱ��
�� ![]()
![]()
���ϣ� ![]() ��
�� ![]() ��
��
��3���⣺��ͼ�ۣ��á�EDO=45�㣮
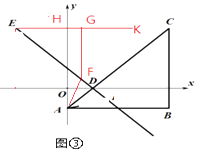
����E��EK��x�ύ ![]() ����H�����KEF=��EDO=45�㣮
����H�����KEF=��EDO=45�㣮
����F��FG��EK�ڵ�G����FG=EG= ![]() ��
��
�����⣬����M�˶���·��Ϊ����AF+EF���˶�ʱ�䣺
![]() ��
��
�� ![]() �����˶�ʱ���������AF+FG�ij��ȣ�
�����˶�ʱ���������AF+FG�ij��ȣ�
�ɴ��߶���̿�֪������AF+FG�ij��ȵ���СֵΪEK���߶�AB֮��Ĵ��߶Σ�
��t��С=AH��AH�� ![]() ��Ľ��㣬��Ϊ����֮F�㣮
��Ľ��㣬��Ϊ����֮F�㣮
��ֱ��DE����ʽΪ�� ![]()
��F��0��1����
��������������F����Ϊ��0��1��ʱ����M�������˶���������ʱ����
����������1����������Ķ���������ɵ�B��D��E�����꣬���ô���ϵ�����������ֱ��DE�Ľ���ʽ���ɡ�
��2���ȸ��ݹ��ɶ����ֱ����AC��AD�ij�����֤����DPGΪ����ֱ�������Σ��ó� s=![]() DP2 .������������ٵ� 0 �� t ��
DP2 .������������ٵ� 0 �� t ��![]() ʱ���ڵ�
ʱ���ڵ�![]() < t �� 4
< t �� 4![]() ʱ���ֱ����DP�ij������ɵó������
ʱ���ֱ����DP�ij������ɵó������
��3������E��EK��x�ύy����H�����KEF=��EDO=45�㣮����F��FG��EK�ڵ�G����FG=EG=![]() EF�������⣬����M�˶���·��Ϊ����AF+EF���˶�ʱ�䣺t=AF+EF���Ƴ�t=AF+FG�����˶�ʱ���������AF+FG�ij��ȣ��ɴ��߶���̿�֪������AF+FG�ij��ȵ���СֵΪEK���߶�AB֮��Ĵ��߶Σ���t��С=AH��ֱ��DE��y��Ľ��㼴Ϊ����֮F�㡣
EF�������⣬����M�˶���·��Ϊ����AF+EF���˶�ʱ�䣺t=AF+EF���Ƴ�t=AF+FG�����˶�ʱ���������AF+FG�ij��ȣ��ɴ��߶���̿�֪������AF+FG�ij��ȵ���СֵΪEK���߶�AB֮��Ĵ��߶Σ���t��С=AH��ֱ��DE��y��Ľ��㼴Ϊ����֮F�㡣

 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�