题目内容
 如图:已知:△ABC中,∠ABC、∠ACB的平分线,交于点O,过点O画EF∥BC交AB于点E,AC于点F.
如图:已知:△ABC中,∠ABC、∠ACB的平分线,交于点O,过点O画EF∥BC交AB于点E,AC于点F.
(1)写出可用图中字母表示的相等的角,并说明理由;
(2)若∠ABC=60°,∠ACB=80°,求∠A、∠BOC的度数;
(3)根据(2)的解答,请你猜出∠BOC与∠A度数的大小关系.
解:(1)∵EF∥BC,
∴∠OBC=∠BOE,∠OCB=∠COF,
又∵BO、CO分别是∠ACB和∠ACB的角平分线,
∴∠OBC=∠OBE,∠OCB=∠FCO,
∴∠BOE=∠OBC=∠OBE,∠COF=∠OCB=∠FCO;
(2)在△ABC中,∵∠ABC=60°,∠ACB=80°,
∴∠A=180°-∠ABC-∠ACB=40°;
∵BO、CO分别是∠ACB和∠ACB的角平分线,
∴∠OBC= ∠ABC=30°,∠OCB=
∠ABC=30°,∠OCB= ∠ACB=40°,
∠ACB=40°,
∴∠BOC=180°-∠OBC-∠OCB=110°;
(3)根据(2)的解答,可猜测出∠BOC与∠A度数的大小关系为:∠BOC=90°+ ∠A.理由如下:
∠A.理由如下:
∵BO、CO分别是∠ABC和∠ACB的角平分线,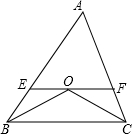
∴∠OBC= ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,
∠ACB,
∴∠BOC=180°-∠OBC-∠OCB=180°- ∠ABC-
∠ABC- ∠ACB=180°-
∠ACB=180°- (∠ABC+∠ACB),
(∠ABC+∠ACB),
又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A,
∴∠BOC=180°- (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A.
∠A.
分析:(1)根据平行线的性质及角平分线的定义得出∠BOE=∠OBC=∠OBE,∠COF=∠OCB=∠FCO;
(2)根据三角形内角和定理可得∠A=180°-∠ABC-∠ACB;先由角平分线的定义求出∠OBC和∠OCB的度数,再根据三角形内角和定理得出∠BOC=180°-∠OBC-∠OCB;
(3)根据(2)的解答,可猜测出∠BOC与∠A度数的大小关系为:∠BOC=90°+ ∠A.
∠A.
点评:本题主要考查了平行线的性质,角平分线的定义及三角形内角和定理,难度中等.
∴∠OBC=∠BOE,∠OCB=∠COF,
又∵BO、CO分别是∠ACB和∠ACB的角平分线,
∴∠OBC=∠OBE,∠OCB=∠FCO,
∴∠BOE=∠OBC=∠OBE,∠COF=∠OCB=∠FCO;
(2)在△ABC中,∵∠ABC=60°,∠ACB=80°,
∴∠A=180°-∠ABC-∠ACB=40°;
∵BO、CO分别是∠ACB和∠ACB的角平分线,
∴∠OBC=
 ∠ABC=30°,∠OCB=
∠ABC=30°,∠OCB= ∠ACB=40°,
∠ACB=40°,∴∠BOC=180°-∠OBC-∠OCB=110°;
(3)根据(2)的解答,可猜测出∠BOC与∠A度数的大小关系为:∠BOC=90°+
 ∠A.理由如下:
∠A.理由如下:∵BO、CO分别是∠ABC和∠ACB的角平分线,

∴∠OBC=
 ∠ABC,∠OCB=
∠ABC,∠OCB= ∠ACB,
∠ACB,∴∠BOC=180°-∠OBC-∠OCB=180°-
 ∠ABC-
∠ABC- ∠ACB=180°-
∠ACB=180°- (∠ABC+∠ACB),
(∠ABC+∠ACB),又∵在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°-∠A,
∴∠BOC=180°-
 (180°-∠A)=90°+
(180°-∠A)=90°+ ∠A.
∠A.分析:(1)根据平行线的性质及角平分线的定义得出∠BOE=∠OBC=∠OBE,∠COF=∠OCB=∠FCO;
(2)根据三角形内角和定理可得∠A=180°-∠ABC-∠ACB;先由角平分线的定义求出∠OBC和∠OCB的度数,再根据三角形内角和定理得出∠BOC=180°-∠OBC-∠OCB;
(3)根据(2)的解答,可猜测出∠BOC与∠A度数的大小关系为:∠BOC=90°+
 ∠A.
∠A.点评:本题主要考查了平行线的性质,角平分线的定义及三角形内角和定理,难度中等.

练习册系列答案
相关题目
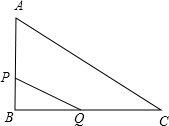
 如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF.
如图,已知:△ABC中,∠1=∠2,且AE=AD,BE和CD相交于F.求证:BF=CF. 如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE.
如图,已知:△ABC为等边三角形,D、F分别为射线BC、射线AB边上的点,BD=AF,以AD为边作等边△ADE. 如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则
如图,已知在△ABC中,AB=AC,∠A=36°,BD为∠ABC的平分线,则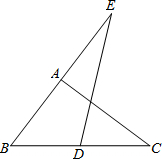 如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,
如图,已知在△ABC中,D是边BC的中点,点E在边BA的延长线上,AE=AB,