Question

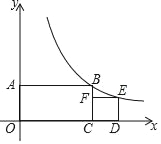
【题目】如图，矩形OABC的一个顶点与坐标原点重合，OC、OA分别在x轴和y轴上，正方形CDEF的一条边在x轴上，另一条边CF在BC上，反比例函数y＝的图象经过B、E两点，已知OA＝2，则正方形的边长是（　　）

A. 2-2 B. C. 4-2 D. 4﹣2

Answer 1

【答案】A

【解析】

依据反比例函数y=的图象经过B点，BC=AO=2，可得B（4，2），设正方形的边长为a，则E（4+a，a），代入反比例函数y=，可得正方形的边长是2-2．

解：∵反比例函数y＝的图象经过B点，BC＝AO＝2，

∴当y＝2时，x＝4，即B（4，2），

设正方形的边长为a，则OD＝4+a，DE＝a，

∴E（4+a，a），

代入反比例函数y＝，可得

a（4+a）＝8，

解得a＝ 2-2或a＝﹣2-2（舍去），

∴正方形的边长是2-2.，

故选：A．