题目内容
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0, ).
).
【小题1】求抛物线的解析式及其顶点D的坐标;
【小题2】设直线CD交x轴于点E,过点B作x轴的垂线,交直线CD于点F,在直线CD的上方,y轴及y轴的右侧的平面内找一点G,使以点G、F、C为顶点的三角形与△COE相似,请直接写出符合要求的点G的坐标;
【小题3】如图,抛物线的对称轴与x轴的交点M,过点M作一条直线交∠ADB于T,N两点,①当∠DNT=90°时,直接写出
 的值;
的值;②当直线TN绕点M旋转时,
试说明: △DNT的面积S△DNT=
 ;
;并猜想 :
 的值是否是定值?说明理由.
的值是否是定值?说明理由.
【小题1】y=
 ,顶点D的坐标(1,
,顶点D的坐标(1,  )
)【小题2】

【小题3】是定值
 解析:
解析:解:抛物线与X轴交于点A(-2,0),B(4,0),与Y轴交于点C(0,
 ),
),故可设抛物线解析式为y=a(x+2)(x-4) (设一般式也可)
则
 =a(0+2)(0-4) ∴a=
=a(0+2)(0-4) ∴a=
抛物线的解析式为:y=
 (x+2)(x-4),即y=
(x+2)(x-4),即y=
化为顶点式:y=

∴顶点D的坐标(1,
 ) 2分
) 2分(2)
 6分
6分(3)①
 7分
7分② i.是定值

理由是:作NH⊥DT于点H,
又∵抛物线是轴对称图形,DM是对称轴,
∴DA=DB,
∵tan∠DAB=

∴∠DAB=60°,
∴△DAB是等边三角形,
∴∠ADB=60°,
∴S△DNT=
 DT·NH=
DT·NH= DT·DN·sin60°=
DT·DN·sin60°= DT·DN 9分
DT·DN 9分ii.方法1:(面积法)
作NH⊥DT于H, MM1⊥DT于M1,MM2⊥DN于M2,
∴NH= DN·sin60°=
 DN,
DN,又∵△DAB是等边三角形,且DM⊥AB于M,
∴∠TDM=∠NDM=30°,
∴MM1 = MM2= DM·sin30°=
 DM,
DM,∵S△DNT=
 DT·DN
DT·DN∵S△DTM+ S△DNM =
 DT·MM1+
DT·MM1+ DN·MM2
DN·MM2=
 DT·DMsin30°+
DT·DMsin30°+ DN·DMsin30
DN·DMsin30=

∵S△DNT=S△DTM+ S△DNM
∴
 DT·DN=
DT·DN=
∴DT·DN=3

∴

 12分
12分方法2:(相似三角形的知识)
作NN1⊥DM于N1,TT1⊥DM于T1,
又∵△DAB是等边三角形,且DM⊥AB于M,
∴∠TDM=∠NDM=30°,
∵∠DN1N=∠TT1D=90°,
∴△DN1N∽△D T1T
∴

又∵∠TMT1=∠NMN1,
∵∠NN1M=∠TT1D=90°,
∴△NN1M∽△TT1M
∴

∴
 =
= =
=
∴


∴

 12分
12分 
练习册系列答案
相关题目
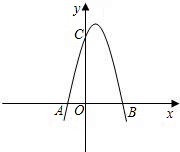 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).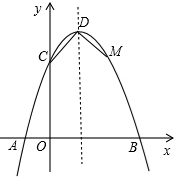 如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1
如图,已知抛物线与x轴交于点A(-1,0),与y轴交于点C(0,3),且对称轴方程为x=1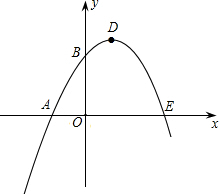 函数的最大值是4.
函数的最大值是4. (2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )
(2012•株洲)如图,已知抛物线与x轴的一个交点A(1,0),对称轴是x=-1,则该抛物线与x轴的另一交点坐标是( )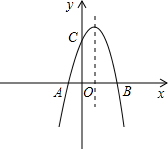 如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).
如图,已知抛物线与x轴交于点A(-2,0),B(4,0),与y轴交于点C(0,8).