题目内容
如图，∠PQR=138°，∠SQR=90°，∠PQT=90°，则∠SQT=________．
42°
分析：由于∠PQT=90°，可知所求∠SQT与∠PQS互余，因此要求∠SQT的度数，只需求出∠PQS的度数即可．易知∠PQS=∠PQR-∠SQR．
解答：∵∠PQS=∠PQR-∠SQR=138°-90°=48°，
∴∠SQT=∠PQT-∠PQS=90°-48°=42°．
故答案为42°．
点评：利用角的和差运算，可将求角的问题逐步转化．
分析：由于∠PQT=90°，可知所求∠SQT与∠PQS互余，因此要求∠SQT的度数，只需求出∠PQS的度数即可．易知∠PQS=∠PQR-∠SQR．
解答：∵∠PQS=∠PQR-∠SQR=138°-90°=48°，
∴∠SQT=∠PQT-∠PQS=90°-48°=42°．
故答案为42°．
点评：利用角的和差运算，可将求角的问题逐步转化．
练习册系列答案
相关题目
在△ABC中， AB、BC、AC三边的长分别为、、，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．
【小题1】△ABC的面积为： ．
【小题2】若△DEF三边的长分别为、2、，请在图2的正方形网格中画出相应的△DEF，并利用构图法求出它的面积．
【小题3】利用第2小题解题方法完成下题：如图3，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13、10、17，且△PQR、△BCR、△DEQ、△AFP的面积相等，求六边形花坛ABCDEF的面积．
【小题1】△ABC的面积为： ．
【小题2】若△DEF三边的长分别为、2、，请在图2的正方形网格中画出相应的△DEF，并利用构图法求出它的面积．
|
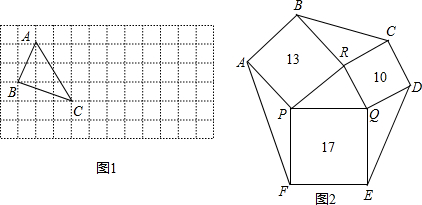
【小题3】利用第2小题解题方法完成下题：如图3，一个六边形的花坛被分割成7个部分，其中正方形PRBA，RQDC，QPFE的面积分别为13、10、17，且△PQR、△BCR、△DEQ、△AFP的面积相等，求六边形花坛ABCDEF的面积．
、
、
，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．
、
、
，请在图1的正方形网格中画出相应的△DEF，并利用构图法求出它的面积；