题目内容
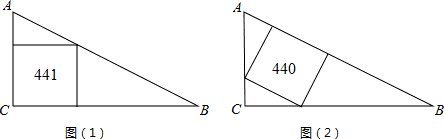
如图Rt△ABC中有两种作内接正方形的方法.图(1)作的内接正方形面积为441,(2)中作的内接正方形的面积为440,则AC+BC的值为
- A.456
- B.458
- C.460
- D.462
D
分析:设BC=a,AC=b,AB=c,先由正方形的性质,可得:EF∥BC,Rt△AFE∽Rt△ACB,再由相似三角形的对应边成比例,可得21(a+b)=ab,然后根据相似三角形面积比等于相似比的平方,用含a、b、c的代数式分别表示图(1)与图(2)中各个三角形的面积,根据△ABC的面积不变,列出方程,结合勾股定理,即可求得AC+BC的值.
解答: 解:如图,设BC=a,AC=b,AB=c.
解:如图,设BC=a,AC=b,AB=c.
在图(1)中,∵四边形EFCD是正方形,
∴EF∥BC,
∴Rt△AFE∽Rt△ACB,
∴EF:BC=AF:AC,21:a=(b-21):b,
∴a+b=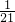 ab.①
ab.①
∵S△AEF:S△ABC=(EF:BC)2,即S△AEF: ab=441:a2,
ab=441:a2,
∴S△AEF= ,
,
同理,S△BDE= .
.
在图(2)中,∵四边形MNPQ是正方形,
∴MQ∥AB,
∴RT△QCM∽Rt△ACB,
∴S△QCM:S△ACB=(QM:AB)2,即S△QCM: ab=440:c2,
ab=440:c2,
∴S△QCM= ,
,
同理,易求S△APQ= ,S△BMN=
,S△BMN= ,
,
∵S△AEF+S△BDE+S正方形CDEF=S△APQ+S△CMQ+S△BMN+S正方形MNPQ=S△ABC,
∴ +
+ +441=
+441= +
+ +
+ +440,
+440,
∴ +
+ +1=
+1= ,
,
∴(a+b)2= ,
,
将①代入上式,整理得c2=440×441.
∵(a+b)2=a2+b2+2ab=440×441+42(a+b),
∴(a+b)2-42(a+b)-440×441=0,
解得:a+b=462(另一个解-420舍去),
∴AC+BC=462.
故选D.
点评:此题考查了正方形的性质和相似三角形的判定与性质,以及勾股定理等知识.此题综合性较强,解题时要注意合理应用数形结合与方程思想.
分析:设BC=a,AC=b,AB=c,先由正方形的性质,可得:EF∥BC,Rt△AFE∽Rt△ACB,再由相似三角形的对应边成比例,可得21(a+b)=ab,然后根据相似三角形面积比等于相似比的平方,用含a、b、c的代数式分别表示图(1)与图(2)中各个三角形的面积,根据△ABC的面积不变,列出方程,结合勾股定理,即可求得AC+BC的值.
解答:
 解:如图,设BC=a,AC=b,AB=c.
解:如图,设BC=a,AC=b,AB=c.在图(1)中,∵四边形EFCD是正方形,
∴EF∥BC,
∴Rt△AFE∽Rt△ACB,
∴EF:BC=AF:AC,21:a=(b-21):b,
∴a+b=
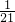 ab.①
ab.①∵S△AEF:S△ABC=(EF:BC)2,即S△AEF:
 ab=441:a2,
ab=441:a2,∴S△AEF=
 ,
,同理,S△BDE=
 .
.在图(2)中,∵四边形MNPQ是正方形,
∴MQ∥AB,
∴RT△QCM∽Rt△ACB,
∴S△QCM:S△ACB=(QM:AB)2,即S△QCM:
 ab=440:c2,
ab=440:c2,∴S△QCM=
 ,
,同理,易求S△APQ=
 ,S△BMN=
,S△BMN= ,
,∵S△AEF+S△BDE+S正方形CDEF=S△APQ+S△CMQ+S△BMN+S正方形MNPQ=S△ABC,
∴
 +
+ +441=
+441= +
+ +
+ +440,
+440,∴
 +
+ +1=
+1= ,
,∴(a+b)2=
 ,
,将①代入上式,整理得c2=440×441.
∵(a+b)2=a2+b2+2ab=440×441+42(a+b),
∴(a+b)2-42(a+b)-440×441=0,
解得:a+b=462(另一个解-420舍去),
∴AC+BC=462.
故选D.
点评:此题考查了正方形的性质和相似三角形的判定与性质,以及勾股定理等知识.此题综合性较强,解题时要注意合理应用数形结合与方程思想.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目


 已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.
已知:如图Rt△ABC中,∠C=Rt∠,AB=5,BC=4.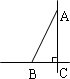
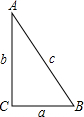
 的点.
的点.