Question

在平面直角坐标系xOy中，直线l的函数解析式为y=-2x，抛物线的函数解析式为y=

1

4

x2-x+6，
①直线y=-2x至少向上平移

 

个单位才能与抛物线y=

1

4

x2-x+6有交点．
②在抛物线上有一个动点A，这个点到直线y=-2x的最短距离是

 

．

Answer 1

分析：①设直线y=-2x至少向上平移 k个单位才能与抛物线y=

1

4

x2-x+6有交点，解y=-2x+k和抛物线组成的方程组，求出b²-4ac即可求出答案；
②设AB=a，A的坐标是（x，

1

4

x²-x+6），A作AC⊥X轴于C，交直线y=-2x于D，过A作AB⊥OB于B，这样得到相似三角形，根据比例式求出A到直线的距离，根据二次函数的特点即可求出其最小值，即得到答案．

解答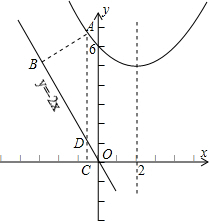：解：①设直线y=-2x至少向上平移 k个单位才能与抛物线y=

1

4

x2-x+6有交点，

y= 1 4 x2-x+6  y=-2x+k

，
即：

1

4

x2-x+6=-2x+k，
∴

1

4

x²+x+6-k=0，
b²-4ac=1²-4•

1

4

•（6-k）≥0，
解得：k≥5，
∴k的最小值是5．
故答案为：5．

②解：如图过A作AC⊥X轴于C，交直线y=-2x于D，过A作AB⊥OB于B，
设AB=a，A的坐标是（x，

1

4

x²-x+6），
则D的横坐标是x，代入y=-2x得：y=-2x，
即：D（x，-2x），C（x，0），
由勾股定理得：OD=-

5

x，
∵∠ABD=∠DCO=90°，∠ADB=∠CDO，
∴△DBA∽△DCO，
∴

AB

OC

=

AD

OD

，
即：

a

-x

=

1 4 x2-x+6-(-2x)

- 5 x

，
解得：a=

5

20

（x+2）²+

5

．

5

20

＞0，a有最小值，
a的最小值是

5

．
故答案为：

5

．

点评：本题主要考查了二次函数的特点，相似三角形的性质和判定，勾股定理，解二元一次方程组等知识点，解此题的关键是通过解方程组得到一个二次函数的解析式求最大值或最小值．题目有一定的难度．