题目内容
如图,已知直线l的函数表达式为y=-| 4 |
| 3 |
 P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点P、Q移动的时间为t秒.
P从A点开始在线段AO上以每秒1个单位长度的速度向点O移动,设点P、Q移动的时间为t秒.(1)当t为何值时,△APQ是以PQ为底的等腰三角形?
(2)求出点P、Q的坐标;(用含t的式子表达)
(3)当t为何值时,△APQ的面积是△ABO面积的
| 1 |
| 5 |
分析:(1)若△APQ是以PQ为底的等腰三角形,那么AQ=AP时,由解析式可得A(6,0),B(0,8),再利用勾股定理得AB=10,然后可以把AQ和AP用t表示,因此得到关于t的方程,解方程即可;
(2)如图,过Q点分别向x轴,y轴引垂线,垂足分别是M,N,设Q(x,y)由题意可知BQ=2t,AP=t,利用△BQN∽△QMA∽△BOA的对应边成比例就可以用t分别表示x、y,也就求出了点P、Q的坐标;
(3)根据(1)(2)知道,△APQ的面积=
AP×QM,△AOB的面积=
×6×8=24,因此可以得到关于t的方程,解方程即可解决问题.
(2)如图,过Q点分别向x轴,y轴引垂线,垂足分别是M,N,设Q(x,y)由题意可知BQ=2t,AP=t,利用△BQN∽△QMA∽△BOA的对应边成比例就可以用t分别表示x、y,也就求出了点P、Q的坐标;
(3)根据(1)(2)知道,△APQ的面积=
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:(1)当AQ=AP时,是以PQ为底的等腰三角形,
解:(1)当AQ=AP时,是以PQ为底的等腰三角形,
∵直线l的函数表达式为y=-
x+8,且l与x轴,y轴分别交于A,B两点,
∴A(6,0),B(0,8),
∴AB=10,
∴AQ=10-2t,AP=t
即10-2t=t,
∴t=
(秒),
当t=
时,是以PQ为底的等腰三角形;
(2)过Q点分别向x轴,y轴引垂线,垂足分别是M,N,
∴NQ∥OA,QM∥OB,
∴△BNQ∽△QMA∽△BOA,
设Q(x,y)
∴BQ=2t,AP=t
而△BQN∽△QMA∽△BOA,
∴
=
,
=
,
∴
=
,
=
,
∴x=
t,y=
(10-2t)
Q,P的坐标分别是[
t,
(10-2t)],(6-t,0);
(3)∵△APQ的面积=
AP×QM
△AOB的面积=
×6×8=24
∴
t×
(10-2t)=
×24
解得,t1=2,t2=3
∴当t1=2秒或,t2=3秒时,△APQ的面积是△ABO面积的
.
 解:(1)当AQ=AP时,是以PQ为底的等腰三角形,
解:(1)当AQ=AP时,是以PQ为底的等腰三角形,∵直线l的函数表达式为y=-
| 4 |
| 3 |
∴A(6,0),B(0,8),
∴AB=10,
∴AQ=10-2t,AP=t
即10-2t=t,
∴t=
| 10 |
| 3 |
当t=
| 10 |
| 3 |
(2)过Q点分别向x轴,y轴引垂线,垂足分别是M,N,
∴NQ∥OA,QM∥OB,
∴△BNQ∽△QMA∽△BOA,
设Q(x,y)
∴BQ=2t,AP=t
而△BQN∽△QMA∽△BOA,
∴
| BQ |
| QN |
| AB |
| OA |
| QA |
| QM |
| AB |
| BO |
∴
| 2t |
| x |
| 10 |
| 6 |
| 10-2t |
| y |
| 10 |
| 8 |
∴x=
| 6 |
| 5 |
| 4 |
| 5 |
Q,P的坐标分别是[
| 6 |
| 5 |
| 4 |
| 5 |
(3)∵△APQ的面积=
| 1 |
| 2 |
△AOB的面积=
| 1 |
| 2 |
∴
| 1 |
| 2 |
| 4 |
| 5 |
| 1 |
| 5 |
解得,t1=2,t2=3
∴当t1=2秒或,t2=3秒时,△APQ的面积是△ABO面积的
| 1 |
| 5 |
点评:本题综合考查了一次函数与几何知识的应用,题中运用平行线的性质、直线的解析式以及直角三角形等知识求出线段的长是解题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图,已知直线l与坐标轴相交于点A(2,0)、B(0,-3).
如图,已知直线l与坐标轴相交于点A(2,0)、B(0,-3).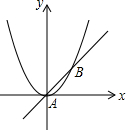 如图,已知直线y=x与抛物线y=
如图,已知直线y=x与抛物线y=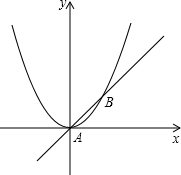 (2013•德宏州)如图,已知直线y=x与抛物线
(2013•德宏州)如图,已知直线y=x与抛物线 (2010•资阳)如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9
(2010•资阳)如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9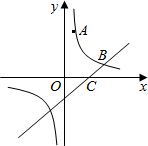 如图,已知反比例函数的图象经过点A,B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0)
如图,已知反比例函数的图象经过点A,B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0)