题目内容
如图,在△ABC中,点D在BC上,在下列四个条件:①∠BAD=∠C;②∠ADC+∠BAC=180°; ③BA2=BD·BC;④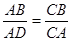 中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】
中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】
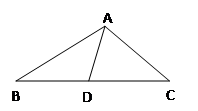
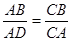 中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】
中能使△BDA∽△BAC的条件有 ……………… ………… …………… …【 】 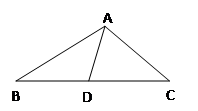
| A.1个 | B.2个 | C.3个 | D.4个 |
C
本题主要考查三角形相似的判定,对于一般的三角形来说,判定方法有三种:(1)两角对应相等两三角形相似. (2)两边对应成比例且夹角相等,两个三角形相似. (3)三边对应成比例,两个三角形相似.∵在△BDA和△BAC中,∠B为公共角,故①∠BAD=∠C可以;
而②∠ADC+∠BAC=180°,∵∠BDA+∠ADC=180°∴∠BAC=∠BDA, 故②可以;对于③BA2=BD·BC,对应两边成比例,他们的夹角恰好是∠B,故根据判定2可以判断;对于④ 他们的夹角为∠BAD和∠C无法判定这两角是否相等,故不能判断,所以共有三个,选择C
他们的夹角为∠BAD和∠C无法判定这两角是否相等,故不能判断,所以共有三个,选择C
而②∠ADC+∠BAC=180°,∵∠BDA+∠ADC=180°∴∠BAC=∠BDA, 故②可以;对于③BA2=BD·BC,对应两边成比例,他们的夹角恰好是∠B,故根据判定2可以判断;对于④
 他们的夹角为∠BAD和∠C无法判定这两角是否相等,故不能判断,所以共有三个,选择C
他们的夹角为∠BAD和∠C无法判定这两角是否相等,故不能判断,所以共有三个,选择C
练习册系列答案
相关题目
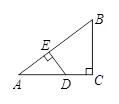
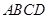 中,
中,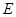 为
为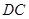 的中点,
的中点,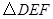 的面积为2,则△
的面积为2,则△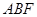 的面积为( )
的面积为( )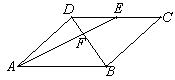
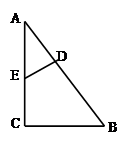
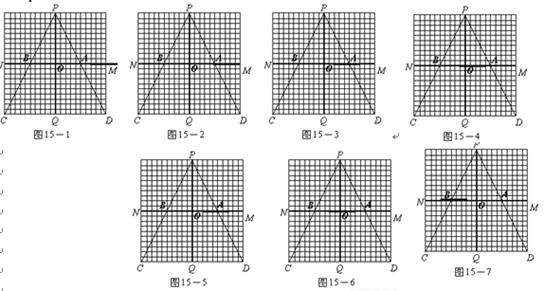
 ,实际该城市面积为320 km
,实际该城市面积为320 km