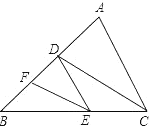
题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,M是AB上的动点
,M是AB上的动点![]() 不与A、B重合
不与A、B重合![]() ,过点M作
,过点M作![]() 交AC于点N,以MN为直径作
交AC于点N,以MN为直径作![]() ,并在
,并在![]() 内作内接矩形
内作内接矩形![]() 设
设![]() .
.
![]() 的面积
的面积![]() ______,
______,![]() ______;
______;![]() 用含x的代数式表示
用含x的代数式表示![]()
![]() 在动点M的运动过程中,设
在动点M的运动过程中,设![]() 与四边形MNCB重合部分的面积为
与四边形MNCB重合部分的面积为![]() 试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?
试求y关于x的函数表达式,并求出x为何值时,y的值最大,最大值为多少?

【答案】(1)![]() ;
;![]() ;(2)y关于x的函数表达式为
;(2)y关于x的函数表达式为 ,当
,当![]() 时,y的值最大,最大值为
时,y的值最大,最大值为![]() .
.
【解析】
![]() 在
在![]() 中,利用勾股定理可求出BC的值,由
中,利用勾股定理可求出BC的值,由![]() ,利用平行线分线段成比例可求出AN、MN的值,再利用三角形的面积公式结合矩形的性质即可求出
,利用平行线分线段成比例可求出AN、MN的值,再利用三角形的面积公式结合矩形的性质即可求出![]() 的面积S的值;
的面积S的值;
![]() 分
分![]() 及
及![]() 两种情况考虑:
两种情况考虑:![]() 当
当![]() 时,利用
时,利用![]() 的结论可得出y关于x的函数关系式,利用二次函数的性质可求出此时y的最大值;
的结论可得出y关于x的函数关系式,利用二次函数的性质可求出此时y的最大值;![]() 当
当![]() 时,由
时,由![]() 可得出BM、PF的值,利用三角形的面积公式结合
可得出BM、PF的值,利用三角形的面积公式结合![]() 可得出y关于x的函数关系式,利用二次函数的性质可求出此时y的最大值
可得出y关于x的函数关系式,利用二次函数的性质可求出此时y的最大值![]() 综上,此题得解.
综上,此题得解.
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() ,
,
![]() ,即
,即![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
![]() 四边形AMPN为矩形,
四边形AMPN为矩形,
![]() .
.
故答案为:![]() ;
;![]()
![]() 当点M为线段AB中点时,点P落在线段BC上,
当点M为线段AB中点时,点P落在线段BC上,
![]() 分
分![]() 及
及![]() 两种情况考虑.
两种情况考虑.
![]() 当
当![]() 时,如图1所示.
时,如图1所示.
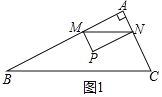
![]() ,
,
![]() ,
,
![]() 当
当![]() 时,y取最大值,最大值为1;
时,y取最大值,最大值为1;
![]() 当
当![]() 时,如图2所示.
时,如图2所示.

![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 当x取
当x取![]() 时,y取最大值,最大值为
时,y取最大值,最大值为![]() .
.
综上所述:y关于x的函数表达式为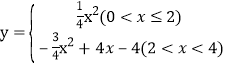 ,
,
当![]() 时,y的值最大,最大值为
时,y的值最大,最大值为![]() .
.

练习册系列答案
相关题目
【题目】某烤鸭店在确定烤鸭的烤制时间时,主要依据的是如表数据:
鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
烤制时间/分钟 | 40 | 60 | 80 | 100 | 120 | 140 | 160 |
设鸭的质量为x千克,烤制时间为t,估计当x=2.2千克时,t的值为_____.